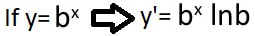Sentry Page Protection
Please Wait...
Lesson 23: Derivatives of Exponential Functions
The derivative of an exponential function is an exponential function. The following relationship holds true, given that k is some constant:
We also know that the value of k is equal to 1 when:
Note that the above is not an exact formula for the derivative of an exponential. It simply emphasizes that the derivative of an exponential function is an exponential function. At this point we should introduce the derivative of the exponential function:
Therefore the derivative of any exponential function is that exponential function multiplied by the natural logarithm of the base. Let us go through some problems:
Take the derivative of each function. Graph it along with the derivative.
y=4^x
y=4^x (ln 4) The base is 4 so multiply by the natural logarithm of 4.
To graph each function, take some ordered pairs for each function. For y=4^x some ordered pairs are:
(-1,0.25), (0,1), (1,4), and (2, 16). To determine another set of ordered pairs for y=4^x (ln 4) simply multiply each y-value with ln 4 (which is approximately 1.386):
(-1,0.35), (0,1.39), (1,5.55), (2,22.18). Now simply plot the points and draw a smooth graph for each function.
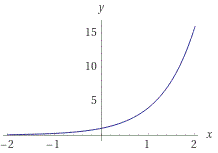
The graph of y=4^x, based on the above points, is shown below:
Take the derivative of each function. Graph it along with the derivative.
y=4^x
y=4^x (ln 4) The base is 4 so multiply by the natural logarithm of 4.
To graph each function, take some ordered pairs for each function. For y=4^x some ordered pairs are:
(-1,0.25), (0,1), (1,4), and (2, 16). To determine another set of ordered pairs for y=4^x (ln 4) simply multiply each y-value with ln 4 (which is approximately 1.386):
(-1,0.35), (0,1.39), (1,5.55), (2,22.18). Now simply plot the points and draw a smooth graph for each function.
The graph of y=4^x, based on the above points, is shown below:
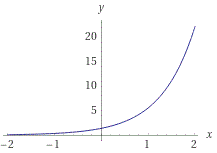
The graph of y=4^x (ln 4), based on the above points, is shown below:
Next let's go through a problem where we will have to find the equation of a tangent line:
Determine the equation of the line that is tangent to the curve y=3e^x at x=ln 5.
We are asked to find the equation of the tangent line at a specific point. We can use this same point of tangency as the point that we will later substitute into the point-slope formula of a line. let us determine the y-coordinate of the point of tangency by substituting x=ln 5 into our curve equation:
y=3e^x First substitute x=ln 5 into the equation of the curve.
y=3e^(ln 5) Here we remember the property e^ln x=x. Therefore e^ln 5=5.
y=3(5)
y=15
Therefore the point of tangency on the curve is (ln 5, 15). Next, we need to find the slope at the tangent at this point of tangency. We can then plug in the point of tangency and this slope into the point-slope formula. To get the slope of the tangent at x=ln 5, take the derivative and solve the derivative for x=ln 5.
y=3e^x
y=3e^x Note that the derivative of e^x is e^x. The 3 remains as the coefficient because of the constant multiple rule.
y=3e^(ln 5) We remember the property e^ln x=x so e^ln 5=5.
y=3(5)
y=15
Therefore the slope of the line tangent to curve at x=ln 5 is 15. We can now plug this slope and the point (ln 5, 15) into the point-slope formula:
y-y₁=m(x-x₁)
y-15=15(x-ln 5) Plug in x₁=ln 5, y₁=15, and m=15.
y=15x-15(ln 5)+15
Therefore the equation of the tangent to the curve y=3e^x at x=ln 5 is y=15x-15(ln 5)+15. Next, we will go over a word problem involving the derivative of an exponential function. Derivatives of exponentials have many uses in solving a variety of problems involving investments and the growth of populations. Let us look at one such problem:
A national park has zoned in a group of 200 rabbits in a fenced in zone. A park warden is responsible for tracking the population. The rabbit population quadruples every month. Determine the number of rabbits in the zone after 4 months. Then determine how fast the rabbit population is increasing when they are initially discovered. Also, determine how fast the rabbit population is increasing after 4 months.
We can write an equation to model the number of rabbits based on the information given. Then, we can determine the number of rabbits after 4 months:
Let P(t) represent the number of rabbits after t months. The equation that models the number of rabbits in the zone after t months is:
P(t)=200(4)^t
To determine the number of rabbits in the zone after four months, substitute t=4 into the equation:
P(t)=200(4)^(4)
P(t)=200(256)
P(t)=51,200
Therefore there are 51,200 rabbits after 4 months. To determine how fast the rabbit population is increasing we will have to take the derivative of P(t). Then, we can plug in different values of t to determine how fast the population is changing at different times.
P(t)=200(4)^t
P'(t)=200(4)^t(ln 4) Take the derivative. Note that the constant multiple rule applies.
Now that we have the derivative, plug in t=0 to determine how fast the rabbit population is increasing initially.
P'(t)=200(4)^t(ln 4)
P'(0)=200(4)^(0)(ln 4)
P'(0)=200(1)(ln 4)
P'(0)≈277
Therefore the rabbit population is initially increasing at a rate of approximately 277 rabbits per month. To determine the rate of increase after 4 months, plug in t=4:
P'(t)=200(4)^t(ln 4)
P'(0)=200(4)^(4)(ln 4)
P'(0)=200(256)(ln 4)
P'(0)≈70,978
Therefore the rabbit population in the zone is increasing at a rate of 70,978 rabbits per months after 4 months. That's all there is to this lesson. Next lesson we will do more derivatives of exponential functions.
Determine the equation of the line that is tangent to the curve y=3e^x at x=ln 5.
We are asked to find the equation of the tangent line at a specific point. We can use this same point of tangency as the point that we will later substitute into the point-slope formula of a line. let us determine the y-coordinate of the point of tangency by substituting x=ln 5 into our curve equation:
y=3e^x First substitute x=ln 5 into the equation of the curve.
y=3e^(ln 5) Here we remember the property e^ln x=x. Therefore e^ln 5=5.
y=3(5)
y=15
Therefore the point of tangency on the curve is (ln 5, 15). Next, we need to find the slope at the tangent at this point of tangency. We can then plug in the point of tangency and this slope into the point-slope formula. To get the slope of the tangent at x=ln 5, take the derivative and solve the derivative for x=ln 5.
y=3e^x
y=3e^x Note that the derivative of e^x is e^x. The 3 remains as the coefficient because of the constant multiple rule.
y=3e^(ln 5) We remember the property e^ln x=x so e^ln 5=5.
y=3(5)
y=15
Therefore the slope of the line tangent to curve at x=ln 5 is 15. We can now plug this slope and the point (ln 5, 15) into the point-slope formula:
y-y₁=m(x-x₁)
y-15=15(x-ln 5) Plug in x₁=ln 5, y₁=15, and m=15.
y=15x-15(ln 5)+15
Therefore the equation of the tangent to the curve y=3e^x at x=ln 5 is y=15x-15(ln 5)+15. Next, we will go over a word problem involving the derivative of an exponential function. Derivatives of exponentials have many uses in solving a variety of problems involving investments and the growth of populations. Let us look at one such problem:
A national park has zoned in a group of 200 rabbits in a fenced in zone. A park warden is responsible for tracking the population. The rabbit population quadruples every month. Determine the number of rabbits in the zone after 4 months. Then determine how fast the rabbit population is increasing when they are initially discovered. Also, determine how fast the rabbit population is increasing after 4 months.
We can write an equation to model the number of rabbits based on the information given. Then, we can determine the number of rabbits after 4 months:
Let P(t) represent the number of rabbits after t months. The equation that models the number of rabbits in the zone after t months is:
P(t)=200(4)^t
To determine the number of rabbits in the zone after four months, substitute t=4 into the equation:
P(t)=200(4)^(4)
P(t)=200(256)
P(t)=51,200
Therefore there are 51,200 rabbits after 4 months. To determine how fast the rabbit population is increasing we will have to take the derivative of P(t). Then, we can plug in different values of t to determine how fast the population is changing at different times.
P(t)=200(4)^t
P'(t)=200(4)^t(ln 4) Take the derivative. Note that the constant multiple rule applies.
Now that we have the derivative, plug in t=0 to determine how fast the rabbit population is increasing initially.
P'(t)=200(4)^t(ln 4)
P'(0)=200(4)^(0)(ln 4)
P'(0)=200(1)(ln 4)
P'(0)≈277
Therefore the rabbit population is initially increasing at a rate of approximately 277 rabbits per month. To determine the rate of increase after 4 months, plug in t=4:
P'(t)=200(4)^t(ln 4)
P'(0)=200(4)^(4)(ln 4)
P'(0)=200(256)(ln 4)
P'(0)≈70,978
Therefore the rabbit population in the zone is increasing at a rate of 70,978 rabbits per months after 4 months. That's all there is to this lesson. Next lesson we will do more derivatives of exponential functions.
© 2020 MyMathEducator.com All Rights Reserved