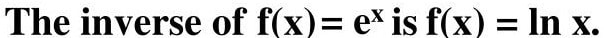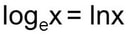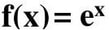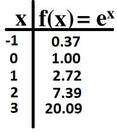Sentry Page Protection
Please Wait...
Lesson 22: The Natural Logarithm
Before we explore the natural logarithm, let us review the number e. The number e is irrational, just like the number π, This means it is a non-repeating, non-terminating number. Its value to 12 decimal places is 2.718281828459. The number is often used as the base of an exponential to model many natural phenomena. In fact, the number is the most often used base within an exponential. The number e (along with the number π) is a transcendental number. This means that a polynomial with integer coefficients cannot be written such that it has e as a root. It is at this point we should introduce the inverse. Its inverse is the natural logarithm function.
The function f(x)= ln x is the natural logarithm function. We note that the natural logarithm is simply a logarithm with base e. (Remember, that a logarithm is asking us how many times do we need to multiply the base by itself to get the number we are after.) Instead of writing log with the base e, we simply write ln x. We pronounce it as "lon" x. Your scientific calculator will have a key 'ln' specially designed for calculations with the natural logarithm.
Let us begin by going over a problem where we will have to graph both functions.
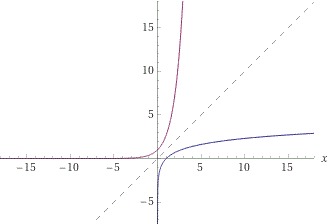
Graph the following function and its inverse. Go over the key features of both functions.
Graph the following function and its inverse. Go over the key features of both functions.
Determine the co-ordinates of several key points. Round your answers and then plot the key points as closely as possible. Then simply reflect the points over the line y=x by switching the x and y co-ordinates for each ordered pair.
Now let us go over the key features of each graph. The graph of y=e^(x) has a domain that is valid over real numbers. Its domain is {x:xεR}. When we look at the graph of y= ln x, we see that its graph is not defined over all real numbers. That is to say, the graph is only defined over value of x that are greater than zero. Therefore its domain is {x:xεR, x>0}. Next, we note that y=e^(x) is not defined over all values of the range. It is the inverse of y= ln x so it makes sense that its range is the domain of y= ln x. Therefore, y=e^x has a range of {y:yεR, y>0}. The function y= ln x is defined for all real values of y and so its range is {y:yεR}. We note that both functions are increasing over their domain. Next we analyze their intercepts. We see above in our table of values that a y-intercept occurs at (0,1) for y=e^x. This is easy to verify because any number to the power of zero has a value of 1. Therefore y=e^x has a y-intercept at y=1. We also note that y=ln x has no y-intercept. We can see that the graph gets closer and closer to the y-axis, but it never actually touches it. We also note that y=e^x gets closer and closer to the x-axis but it never actually touches the x-axis. This means that y=e^x has no x-intercept. If we look at the graph of y=ln x, we see that it does have an x-intercept. Because, it is the inverse of y=e^x, we can confidently say that it has all the same points, except that for each point the x and y-coordinate are switched. Since y=e^x has a y-coordinate at (0,1), y=lnx must have an x-coordinate at (1,0). This can easily be verified:
y=ln x
y=ln (1) Substitute x=1 into the function. Use your calculator to get the answer.
y=0
Therefore the function y=ln x has an x-coordinate at x=1. Next we must state any asymptotes. From the graph we can see that y=e^x has the x-axis as a horizontal asymptote, because its graph gets closer and closer to it but never actually touches it. Therefore y=e^x has a horizontal asymptote at y=0. We also note that the function y=ln x gets closer and closer to the y-axis but does not actually touch it. Therefore y=ln x has a vertical asymptote at x=0. Next, we must check for minima/maxima and points of inflection. The graph of y=e^x increases sharply and has no local maxima or minima. The graph of y=ln x increases gradually and has no local maxima or minima. Next we will check for points of inflection. We see that the second derivative is increasing continuously for y=e^x. Because the second derivative is always positive, there is no point of inflection. We also note that the second derivative is continuously decreasing over the entire domain of y= ln x. Because there is no change in the behavior of the second derivative, there is no point of inflection in y=ln x. Last of all, we check the graphs for concavity. By looking at the graph of y=e^x , we find that it is concave up over its entire domain. By looking at the graph of y=ln x we find that it is concave down over its entire domain. Now that we are fully familiar with y=e^x and y=ln x, let us run through some simple problems. Note that we will have to use our scientific calculators. These calculators have dedicated keys for e, for ln, and for log.
Evaluate correct to four decimal places.
e^(-2)
Simply take the value given and input it into your calculator to get the correct answer:
e^(-2)
=0.1353
Next, we will go though another one of these types of problems:
Evaluate ln 7 to two decimal places.
ln 7
=1.95 Use a scientific calculator.
We note that the following two properties hold true because of the inverse relationship between y=e^x and y=ln x. In the first relationship, we are effectively asking how many times e must be 'multiplied by itself' (remember that ln is a logarithm with a base e but the e is invisible) to get e^x. Of course, the answer is x times. We also note that the second property can be proven true by taking the logarithm of both sides:
e^[ln x]=x
ln e^[ln x]= ln x Take the natural logarithm of both sides.
ln x (ln e) =ln x Remember the logarithm rule log a^(x)= x log a. It also applies to the natural logarithm, as with all rules. Apply it.
ln x (1)= ln x Note that ln e=1. Note that the base e must be multiplied by itself once to get e.
ln x= ln x We have proven the property.
y=ln x
y=ln (1) Substitute x=1 into the function. Use your calculator to get the answer.
y=0
Therefore the function y=ln x has an x-coordinate at x=1. Next we must state any asymptotes. From the graph we can see that y=e^x has the x-axis as a horizontal asymptote, because its graph gets closer and closer to it but never actually touches it. Therefore y=e^x has a horizontal asymptote at y=0. We also note that the function y=ln x gets closer and closer to the y-axis but does not actually touch it. Therefore y=ln x has a vertical asymptote at x=0. Next, we must check for minima/maxima and points of inflection. The graph of y=e^x increases sharply and has no local maxima or minima. The graph of y=ln x increases gradually and has no local maxima or minima. Next we will check for points of inflection. We see that the second derivative is increasing continuously for y=e^x. Because the second derivative is always positive, there is no point of inflection. We also note that the second derivative is continuously decreasing over the entire domain of y= ln x. Because there is no change in the behavior of the second derivative, there is no point of inflection in y=ln x. Last of all, we check the graphs for concavity. By looking at the graph of y=e^x , we find that it is concave up over its entire domain. By looking at the graph of y=ln x we find that it is concave down over its entire domain. Now that we are fully familiar with y=e^x and y=ln x, let us run through some simple problems. Note that we will have to use our scientific calculators. These calculators have dedicated keys for e, for ln, and for log.
Evaluate correct to four decimal places.
e^(-2)
Simply take the value given and input it into your calculator to get the correct answer:
e^(-2)
=0.1353
Next, we will go though another one of these types of problems:
Evaluate ln 7 to two decimal places.
ln 7
=1.95 Use a scientific calculator.
We note that the following two properties hold true because of the inverse relationship between y=e^x and y=ln x. In the first relationship, we are effectively asking how many times e must be 'multiplied by itself' (remember that ln is a logarithm with a base e but the e is invisible) to get e^x. Of course, the answer is x times. We also note that the second property can be proven true by taking the logarithm of both sides:
e^[ln x]=x
ln e^[ln x]= ln x Take the natural logarithm of both sides.
ln x (ln e) =ln x Remember the logarithm rule log a^(x)= x log a. It also applies to the natural logarithm, as with all rules. Apply it.
ln x (1)= ln x Note that ln e=1. Note that the base e must be multiplied by itself once to get e.
ln x= ln x We have proven the property.
Both of these properties are useful in solving equations because they illustrate the relationship between the letter e and the natural logarithm. Let us dive into a word problem.
A scientist is testing for the number of bacteria in a particular colony. The population of bacteria in the colony after t days is given by the following equation.
P(t)=400e^[0.095t]. First, determine the initial population of the colony. Then determine the population after 4 days. Determine how long it will take the population to double. Finally, re-write as an exponential with a base of 2.
First we must determine the initial population of the colony. To do this, set t=0 and solve:
P(t)=400e^[0.095t]
P(0)=400e^[0.095(0)]
P(0)=400e^(0)
P(0)=400(1)
P(0)=400
Therefore the initial bacteria population is 400. Next we must determine the population after 4 days. To do this simply substitute t=4 into our function:
P(t)=400e^[0.095t]
P(4)=400e^[0.095(4)]
P(4)=400e^[0.38]
P(4)=400(1.4623)
P(4)≈585
After 4 days, the population of bacteria is approximately 585. Next we must determine how long it takes for the population to double. We already know that the initial population is 400. If we double this amount, we get 800. Let P(t)=800 and solve for t:
P(t)=400e^[0.095t]
800=400e^[0.095t] Let P(t)=800 and solve.
2=e^[0.095t] Divide both sides by 400.
ln 2= [0.095t] ln e Take the natural logarithm of both sides. Remember, ln e^(x) is equal to x ln e. This is a logarithm rule.
ln 2= [0.095t][1] Note that ln e is equal to 1 because e¹=e.
ln 2=0.095t Isolate t.
t=ln 2/0.095
t=7.30
Therefore the population of bacteria in the colony will double after approximately 7.3 days. For the last part of the problem, we have to re-write as an exponential with a base of 2. First we note that an exponential with base 2 denotes a doubling population. As a result, we will need to express the number of days elapsed in terms of doubling periods. We know that the initial population is 400 and that the population doubles approximately every 7.3 days. Therefore a rewritten equation of P(t), where P is the population of bacteria and t is the time in days is:
P(t)=400(2)^[t/7.3]
Note that the critical component was knowing that we had to express the doubling period as t/7.3. That's all there is to this lesson. Keep in mind that y= ln x and y=e^x are inverse functions and that all logarithm rules still apply to the natural logarithm.
A scientist is testing for the number of bacteria in a particular colony. The population of bacteria in the colony after t days is given by the following equation.
P(t)=400e^[0.095t]. First, determine the initial population of the colony. Then determine the population after 4 days. Determine how long it will take the population to double. Finally, re-write as an exponential with a base of 2.
First we must determine the initial population of the colony. To do this, set t=0 and solve:
P(t)=400e^[0.095t]
P(0)=400e^[0.095(0)]
P(0)=400e^(0)
P(0)=400(1)
P(0)=400
Therefore the initial bacteria population is 400. Next we must determine the population after 4 days. To do this simply substitute t=4 into our function:
P(t)=400e^[0.095t]
P(4)=400e^[0.095(4)]
P(4)=400e^[0.38]
P(4)=400(1.4623)
P(4)≈585
After 4 days, the population of bacteria is approximately 585. Next we must determine how long it takes for the population to double. We already know that the initial population is 400. If we double this amount, we get 800. Let P(t)=800 and solve for t:
P(t)=400e^[0.095t]
800=400e^[0.095t] Let P(t)=800 and solve.
2=e^[0.095t] Divide both sides by 400.
ln 2= [0.095t] ln e Take the natural logarithm of both sides. Remember, ln e^(x) is equal to x ln e. This is a logarithm rule.
ln 2= [0.095t][1] Note that ln e is equal to 1 because e¹=e.
ln 2=0.095t Isolate t.
t=ln 2/0.095
t=7.30
Therefore the population of bacteria in the colony will double after approximately 7.3 days. For the last part of the problem, we have to re-write as an exponential with a base of 2. First we note that an exponential with base 2 denotes a doubling population. As a result, we will need to express the number of days elapsed in terms of doubling periods. We know that the initial population is 400 and that the population doubles approximately every 7.3 days. Therefore a rewritten equation of P(t), where P is the population of bacteria and t is the time in days is:
P(t)=400(2)^[t/7.3]
Note that the critical component was knowing that we had to express the doubling period as t/7.3. That's all there is to this lesson. Keep in mind that y= ln x and y=e^x are inverse functions and that all logarithm rules still apply to the natural logarithm.
© 2020 MyMathEducator.com All Rights Reserved