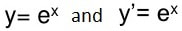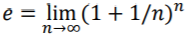Lesson 21: Rates of Change and the Number e

Exponential functions are used in many areas in science and in business. Some examples of exponential functions are included below:
  • The population of rats in a rat farm triples every n days. Then, a function to model the population of the rats is P(t)=I[(3)^(t/n)], where I stands for the initial population, and P represents the current population after t days. 
  • In the function M(x)=I[(1/2)^(x)], M represents the amount of remaining radioactive material, in grams, after x half-life periods, if I is the initial amount of radioactive material, in grams.
  • In the function V(t)=10,000[(1.12)^(t)] $10,000 is earning compound interest in an account at a rate of 12% per year. V represents the value of the investment after t year.
The derivative of an exponential is also an exponential function. We will explore these functions in more depth in the coming chapters. You should be aware that the derivative of an exponential function is a function that is a vertical stretch or compression of the original function. We will look more at exponential functions and their derivatives in the coming lessons. 

Here we are introduced to a number that is commonly found in various forms in nature. The number e is an irrational number that lies between 2.71 and 2.72. The number e is special because the derivative of e raised to the power x is also e raised to the power of x. 
Picture
The value of e is irrational, meaning that e cannot be written as a fraction. The exact value of e is given by the limit:
Picture
That's all there is to this lesson. In the next lesson, we will look at the inverse function of the number e.
© 2020 MyMathEducator.com All Rights Reserved