Sentry Page Protection
Please Wait...
Lesson 20: Applications of Sinusoidal Functions and their Derivatives
,Sinusoidal functions and their derivatives have many applications in every day life. Such everyday applications include engine pistons, alternating electric currents, and oscillating springs. Another common example is the pendulum. Pendulums have been used for centuries because their path is so regular. The displacement of the pendulum can be modelled using a sinusoidal function. Also, the first derivative will give the velocity of the pendulum and the second derivative will give its acceleration. By studying the equations and graphs of sinusoidal functions and their derivatives, we can gain a lot of information about the real world situations they model. Let's look at a word problem involving electricity:
In an AC-DC Circuit a voltage signal is made up of an alternating current (AC) and of a direct current (DC). If t is time in seconds, then voltage, in volts at time t, can be represented by the function V(t)=6 sin t +10. Determine the maximum and minimum voltages and the times at which they occur. Determine the period, T, in seconds and the frequency, f, in hertz. Finally, also determine the amplitude, A, in volts.
To determine where the maximum and minimum occurs for our function, it is necessary to take the first derivative of V(t) and solve by setting it equal to zero.
V(t)=6 sin t +10
V'(t)=6 cos t
0=6 cos t Set the derivative equal to zero.
0=cos t
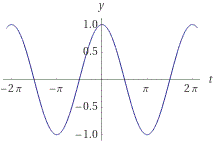
Here we can utilize the graph of y=cos t or we can utilize the unit circle to determine the solutions. Let us utilize the graph.
In an AC-DC Circuit a voltage signal is made up of an alternating current (AC) and of a direct current (DC). If t is time in seconds, then voltage, in volts at time t, can be represented by the function V(t)=6 sin t +10. Determine the maximum and minimum voltages and the times at which they occur. Determine the period, T, in seconds and the frequency, f, in hertz. Finally, also determine the amplitude, A, in volts.
To determine where the maximum and minimum occurs for our function, it is necessary to take the first derivative of V(t) and solve by setting it equal to zero.
V(t)=6 sin t +10
V'(t)=6 cos t
0=6 cos t Set the derivative equal to zero.
0=cos t
Here we can utilize the graph of y=cos t or we can utilize the unit circle to determine the solutions. Let us utilize the graph.
We note when the zeros occur. They occur at [...,-3π/2,-π/2,π/2,3π/2...]. That is, in notation the zeros occur at [t:t=(2k+1)π/2, k∈Z].
Next, let us find what the exact maximum and minimum voltage is and the exact times they occur. We already determine the zeros. By analyzing the zero at x=π/2, we can determine if we are dealing with a local maximum or a local minimum. We note that the slope of the graph is negative at x=π/2. This denotes that the second derivative at this point is negative. However, we know that a local maximum or local minimum occurs on the original graph because the first derivative has a slope of zero. Since the second derivative is negative at this point, the function is concave down and so a local maximum occurs at this point.
We can repeat the analysis for x=3π/2. Because the function of the derivative has a positive slope at this point, the slope of the second derivative would be positive at this point. This tells us that the original function is concave up and so a local minimum occurs at this point. Note that the period of the original function is 2π since no horizontal stretching or compression has taken place, so the local maximums and minimums occur in multiples of 2π. Let us calculate the values of the function at these maxima and minima:
V(t)=6 sin t +10
V(π/2)=6 sin (π/2) +10
V(π/2)=6(1) +10
V(π/2)=16
V(t)=6 sin t +10
V(3π/2)=6 sin (3π/2)+10
V(3π/2)=6 (-1) +10
V(3π/2)=-6+10
V(3π/2)=4
We already noted that one maximum occurred at t=π/2. Since the period of our sine function is 2π and since a sinusoidal function repeats its y-value periodically (that is to say every cycle of its period), we note that the maximum occurs at π/2+2πx, for multiples of x. Likewise, we noted that the minimum occurred at 3π/2. Again, due to the periodicity of the sine function, we note that the minimum occurs at 3π/2+2πx, for multiples of x. Therefore, we can summarize that the maximum voltage of 16 V occurs at t=π/2+2πk s, k∈Z where Z stands for the set of integers. We can also summarize that the minimum voltage of 4 V occurs at t=3π/2+2πk s, k∈Z where Z stands for the set of integers.
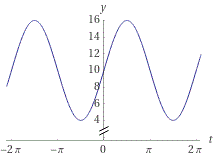
Note that another method to get to the same answer would be to utilize the graph of V(t), after all relevant transformations, and visually analyze for the maximum and minimum. The base function y=sin x is stretched vertically by a factor of 6 and is shifted upwards 10 units. Here we note that there is no horizontal transformation. As a result, all maximums are where they would be on the base sine function. We see clearly from the graph of V(t) (below) that the maximum occur at π/2. Furthermore, we note that the minimum occurs exactly at the same value of t as on the base sine function. That is to say, the minimum occurs at 3π/2. Because there are no horizontal transformations, all maximums and minimums repeat periodically, over a period of 2π (repeat every π/2). From the graph we see that the maximum is 16 and the minimum is 4. Note that this makes sense in terms of the stretch vertically by six units and the shift upward 10 units. On the base sine function the maximum would be 1 but (1×6)+10=16. Likewise, the base sine function would have a minimum of -1 but (-1×6)+10=4. Therefore, we can summarize that the maximum voltage of 16 V occurs at t=π/2+2πk s, k∈Z where Z stands for the set of integers. We can also summarize that the minimum voltage of 4 V occurs at t=3π/2+2πk s, k∈Z where Z stands for the set of integers.
V(π/2)=6 sin (π/2) +10
V(π/2)=6(1) +10
V(π/2)=16
V(t)=6 sin t +10
V(3π/2)=6 sin (3π/2)+10
V(3π/2)=6 (-1) +10
V(3π/2)=-6+10
V(3π/2)=4
We already noted that one maximum occurred at t=π/2. Since the period of our sine function is 2π and since a sinusoidal function repeats its y-value periodically (that is to say every cycle of its period), we note that the maximum occurs at π/2+2πx, for multiples of x. Likewise, we noted that the minimum occurred at 3π/2. Again, due to the periodicity of the sine function, we note that the minimum occurs at 3π/2+2πx, for multiples of x. Therefore, we can summarize that the maximum voltage of 16 V occurs at t=π/2+2πk s, k∈Z where Z stands for the set of integers. We can also summarize that the minimum voltage of 4 V occurs at t=3π/2+2πk s, k∈Z where Z stands for the set of integers.
Note that another method to get to the same answer would be to utilize the graph of V(t), after all relevant transformations, and visually analyze for the maximum and minimum. The base function y=sin x is stretched vertically by a factor of 6 and is shifted upwards 10 units. Here we note that there is no horizontal transformation. As a result, all maximums are where they would be on the base sine function. We see clearly from the graph of V(t) (below) that the maximum occur at π/2. Furthermore, we note that the minimum occurs exactly at the same value of t as on the base sine function. That is to say, the minimum occurs at 3π/2. Because there are no horizontal transformations, all maximums and minimums repeat periodically, over a period of 2π (repeat every π/2). From the graph we see that the maximum is 16 and the minimum is 4. Note that this makes sense in terms of the stretch vertically by six units and the shift upward 10 units. On the base sine function the maximum would be 1 but (1×6)+10=16. Likewise, the base sine function would have a minimum of -1 but (-1×6)+10=4. Therefore, we can summarize that the maximum voltage of 16 V occurs at t=π/2+2πk s, k∈Z where Z stands for the set of integers. We can also summarize that the minimum voltage of 4 V occurs at t=3π/2+2πk s, k∈Z where Z stands for the set of integers.
Next, we are asked to compute the period, T, in seconds, and the frequency, f, in hertz. Since the function has not undergone any horizontal transformations, we note clearly that the period must be the same as the period of a base function. Therefore the period is 2π seconds. The frequency can be easily calculated because frequency is the reciprocal of period.
f=1/T
f=1/2π hertz
Therefore the frequency is equal to 1/2π hertz. Finally, we are asked to also determine the amplitude, A, in volts. We recall that the amplitude is simply one half of the maximum of the function minus the minimum of the function.
A=(Vmax-Vmin)/2
A=(16-4)/2
A=(12)/2
A=6
Therefore the amplitude is equal to 6 V. Next let's go over simple harmonic motion and a word problem that involves simple harmonic motion. Simple harmonic motion. An example of simple harmonic motion (not taking into account the force of friction) is a pendulum. Simple harmonic motion can be modelled by a sinusoidal graph with a constant amplitude. Let's go through a sample word problem dealing with simple harmonic motion.
The period of a simple pendulum depends only on its length. The period of the pendulum can be modelled by the function, T=2π√[l/g], where T is the period, in seconds, l is the length of the pendulum, in meters, and g is the acceleration due to gravity, which has a constant value of 9.8 m/s² on the surface of the earth. The function, h(t)=A cos (2πt/T), for the horizontal position of the bob over time, is an example of simple harmonic motion. In the function, A represents the amplitude of the pendulum in centimeters, t is time, in seconds, and T represents the period of the pendulum, also in seconds. Determine the maximum speed of the bob, and the time when it first occurs, assuming a pendulum length of 1.0 m and an amplitude of 10 cm.
First we must find the period with the period function given in the question. Then we can substitute the period we calculate into the position function, h(t).
T=2π√[l/g] The length of the pendulum is 1.0 m and g is the constant 9.8 m/s².
T=2π√[1.0/9.8]
T=2π√[0.10]
T=2.0 s
The period of the pendulum is 2.0 s. Now we can substitute the period, along with the amplitude given in the problem, into the displacement function h(t).
h(t)=A cos (2πt/T) Amplitude is expressed in centimeters.
h(t)=10 cos (2πt/2.0) Note that T=2.0 s and A is equal to 10 cm.
h(t)=10 cos πt Simplify.
Now take the derivative of this function to get the velocity function.
h(t)=10 cos πt
h'(t)=10π (-sin πt)
h'(t)=-10π sin πt
v(t)=-10π sin πt Let v(t) represent the horizontal velocity of the bob at time t. We note that v(t)=h'(t).
If v(t) is the horizontal velocity of the bob at time t, then v(t)=-10π sin πt. We note that the function has a negative coefficient because on the first swing of the pendulum, the pendulum is going in the negative direction. Therefore, the first point of maximum speed will have a negative velocity. To find the maximum horizontal velocity we need to know at what point v(t) has a slope of zero. To do this, take the derivative of v(t), equate it with zero and solve.
v(t)=-10π sin πt
v'(t)=-10π×π cos πt
v'(t)=-10π² cos πt
a(t)=-10π² cos πt Let a(t) represent the horizontal acceleration of the bob at time t. We note that a(t)=v'(t).
Now, to find the maximum horizontal velocity set a(t) equal to zero and solve:
0=-10π² cos πt
0= cos πt
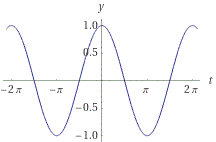
To solve the equation above, determine the earliest solution for a base cosine function. By looking at the graph below we find that the earliest positive solution occurs at π/2. Therefore we can solve for the zero in the equation above by allowing π/2 to equal πt:
f=1/T
f=1/2π hertz
Therefore the frequency is equal to 1/2π hertz. Finally, we are asked to also determine the amplitude, A, in volts. We recall that the amplitude is simply one half of the maximum of the function minus the minimum of the function.
A=(Vmax-Vmin)/2
A=(16-4)/2
A=(12)/2
A=6
Therefore the amplitude is equal to 6 V. Next let's go over simple harmonic motion and a word problem that involves simple harmonic motion. Simple harmonic motion. An example of simple harmonic motion (not taking into account the force of friction) is a pendulum. Simple harmonic motion can be modelled by a sinusoidal graph with a constant amplitude. Let's go through a sample word problem dealing with simple harmonic motion.
The period of a simple pendulum depends only on its length. The period of the pendulum can be modelled by the function, T=2π√[l/g], where T is the period, in seconds, l is the length of the pendulum, in meters, and g is the acceleration due to gravity, which has a constant value of 9.8 m/s² on the surface of the earth. The function, h(t)=A cos (2πt/T), for the horizontal position of the bob over time, is an example of simple harmonic motion. In the function, A represents the amplitude of the pendulum in centimeters, t is time, in seconds, and T represents the period of the pendulum, also in seconds. Determine the maximum speed of the bob, and the time when it first occurs, assuming a pendulum length of 1.0 m and an amplitude of 10 cm.
First we must find the period with the period function given in the question. Then we can substitute the period we calculate into the position function, h(t).
T=2π√[l/g] The length of the pendulum is 1.0 m and g is the constant 9.8 m/s².
T=2π√[1.0/9.8]
T=2π√[0.10]
T=2.0 s
The period of the pendulum is 2.0 s. Now we can substitute the period, along with the amplitude given in the problem, into the displacement function h(t).
h(t)=A cos (2πt/T) Amplitude is expressed in centimeters.
h(t)=10 cos (2πt/2.0) Note that T=2.0 s and A is equal to 10 cm.
h(t)=10 cos πt Simplify.
Now take the derivative of this function to get the velocity function.
h(t)=10 cos πt
h'(t)=10π (-sin πt)
h'(t)=-10π sin πt
v(t)=-10π sin πt Let v(t) represent the horizontal velocity of the bob at time t. We note that v(t)=h'(t).
If v(t) is the horizontal velocity of the bob at time t, then v(t)=-10π sin πt. We note that the function has a negative coefficient because on the first swing of the pendulum, the pendulum is going in the negative direction. Therefore, the first point of maximum speed will have a negative velocity. To find the maximum horizontal velocity we need to know at what point v(t) has a slope of zero. To do this, take the derivative of v(t), equate it with zero and solve.
v(t)=-10π sin πt
v'(t)=-10π×π cos πt
v'(t)=-10π² cos πt
a(t)=-10π² cos πt Let a(t) represent the horizontal acceleration of the bob at time t. We note that a(t)=v'(t).
Now, to find the maximum horizontal velocity set a(t) equal to zero and solve:
0=-10π² cos πt
0= cos πt
To solve the equation above, determine the earliest solution for a base cosine function. By looking at the graph below we find that the earliest positive solution occurs at π/2. Therefore we can solve for the zero in the equation above by allowing π/2 to equal πt:
πt=π/2 We are doing this to solve 0= cos πt.
t=0.5 s
After 0.5 seconds is when the maximum horizontal velocity is reached. Note that it makes sense based on the graph of displacement because at the zero the graph has the steepest slope. Let us substitute t=0.5 s into the velocity function to determine the velocity at this time.
t=0.5 s
After 0.5 seconds is when the maximum horizontal velocity is reached. Note that it makes sense based on the graph of displacement because at the zero the graph has the steepest slope. Let us substitute t=0.5 s into the velocity function to determine the velocity at this time.
v(t)=-10π sin πt
v(0.5)=-10π sin π(0.5)
v(0.5)=-10π sin (π/2)
v(0.5)=-10π (1)
v(0.5)=-10π
v(0.5)=-31.42 m/s
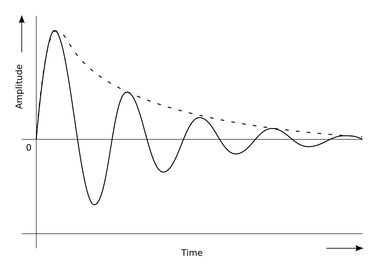
Therefore the maximum velocity of the pendulum occurs after 0.5 seconds and is -31.42 m/s. Note the direction is negative because the pendulum is moving in the direction opposite of initial displacement. That is, the pendulum had to be pushed in one direction to begin and the maximum velocity is reached as it moves in the other, negative direction. Note that in our example, friction had no effect on the amplitude of our pendulum. When friction acts upon an oscillating pendulum, its amplitude will diminish over time. Such harmonic motion (where amplitude diminishes over time) is called damped harmonic motion. The graph below illustrates damped harmonic motion. That's all there is to this lesson. Keep in mind that the second derivative test (used in the first problem) also applies to sinusoidal functions.
v(0.5)=-10π sin π(0.5)
v(0.5)=-10π sin (π/2)
v(0.5)=-10π (1)
v(0.5)=-10π
v(0.5)=-31.42 m/s
Therefore the maximum velocity of the pendulum occurs after 0.5 seconds and is -31.42 m/s. Note the direction is negative because the pendulum is moving in the direction opposite of initial displacement. That is, the pendulum had to be pushed in one direction to begin and the maximum velocity is reached as it moves in the other, negative direction. Note that in our example, friction had no effect on the amplitude of our pendulum. When friction acts upon an oscillating pendulum, its amplitude will diminish over time. Such harmonic motion (where amplitude diminishes over time) is called damped harmonic motion. The graph below illustrates damped harmonic motion. That's all there is to this lesson. Keep in mind that the second derivative test (used in the first problem) also applies to sinusoidal functions.
© 2020 MyMathEducator.com All Rights Reserved