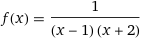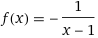Sentry Page Protection
Please Wait...
Lesson 15: Simple Rational Functions
In this lesson we will be exploring rational functions. One property of rational functions is that they have vertical asymptotes. In general, the denominator of a rational function cannot be equal to zero. That is to say equating a denominator to zero and solving for x will yield the vertical asymptote of a rational function. Such a rational function is undefined at the vertical asymptote or asymptotes. More mathematically, we can say:
- The line x=a is a vertical asymptote if the value of the function approaches infinity, f(x)→±∞, as x→a from the left and/or right.
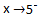
This is a left hand side limit and it is read "x approaches 5 from the left". Note that the negative superscript denotes that the number 5 is being approached from the left side. This means that x takes on such values as 4.8, 4.9, 4.99, 4.999...
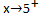
This is a right hand side limit and it is read as "x approaches 5 from the right". Note that the positive superscript denotes that the number 5 is being approached from the right side. This means that x is taking on such values as 5.2, 5.1, 5.01, 5.001...
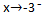
This is also a left hand side limit. It is read as "x approaches -3 from the left". Keep in mind this is a negative (visualize a number line if needed) so values from the left will be -3.1, -3.01, -3.001...
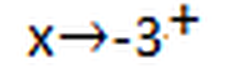
This is a right hand limit and it is read as "x approaches -3 from the right". Keep in mind this is a negative (visualize a number line if needed) so values from the left are -2.9, -2.99, -2.999...
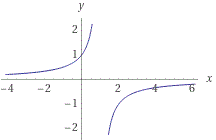
Given the following function, determine the vertical asymptotes. Then find the one sided limits as the x-values approach the vertical asymptotes. Finally, sketch a graph of the function.
xWe know that the denominator of f(x) cannot equal zero because division by zero is undefined. Form above, we know that equating the denominator to zero will give us our vertical asymptotes:
(x-1)(x+2)=0
x-1=0 or x+2=0
x=1 or x=-2
Therefore the vertical asymptotes are x=1 and x=-2. Next we are asked to determine the one sided limits as x-values approach the vertical asymptotes. That is, for each vertical asymptote, we are being asked what is occurring as x approaches from either side. One method of solving this is to use limits. The other method would be to substitute a value that is very close to the vertical asymptote and check the result. We will use limits on the asymptote x=1:
(x-1)(x+2)=0
x-1=0 or x+2=0
x=1 or x=-2
Therefore the vertical asymptotes are x=1 and x=-2. Next we are asked to determine the one sided limits as x-values approach the vertical asymptotes. That is, for each vertical asymptote, we are being asked what is occurring as x approaches from either side. One method of solving this is to use limits. The other method would be to substitute a value that is very close to the vertical asymptote and check the result. We will use limits on the asymptote x=1:
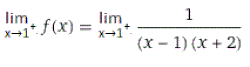
First we begin with the right hand limit. We substitute 1 into x+2, but for x-1 we must consider the limit because this is the asymptote for which we are analyzing the one sided limit. We must think that we are substituting in a value that is approaching 1 from the right side. We get a very small positive number, which we take into account in our calculations.
=1/[(very small positive number)(1+2)]
=1/[(very small positive number)(3)]
=1/(very small positive number) 1 divided by a very small number is infinity. The number is positive.
=+∞
Therefore, as x approaches the asymptote x=1 from the right, the function approaches a very large positive number or +∞. Let us repeat the process, but for the left hand limit:
=1/[(very small positive number)(3)]
=1/(very small positive number) 1 divided by a very small number is infinity. The number is positive.
=+∞
Therefore, as x approaches the asymptote x=1 from the right, the function approaches a very large positive number or +∞. Let us repeat the process, but for the left hand limit:
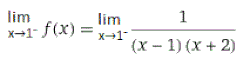
Again, we substitute 1 into x+2 while considering the one sided limit for x-1. We consider that we are substituting a value which is very close to 1 from the left side. That is, a value which is only slightly less than 1. We get a very small negative number.
=1/[(very small negative number)(1+2)]
=1/[(very small negative number)(3)]
=1/(very small negative number)
=-∞
=1/[(very small negative number)(3)]
=1/(very small negative number)
=-∞
Therefore as x approaches the asymptote x=1 from the left, the function approaches a very large negative number or -∞. Now let us proceed to the next asymptote of x=-2. For this asymptote, let us use the second method, which consists of substituting values very close the vertical asymptote and then checking the result.
f(x)=1/[(x-1)(x+2)]
f(-2.01)=1/((-2.01)-1)((-2.01)+2)]
f(-2.01)=1/[(-3.01)(-0.01)]
f(-2.01)=33.22 This is equivalent to a very large positive number. A number closer to 2 would have given us a larger number.
Therefore as x approaches the asymptote x=-2 from the left, the function approaches a very large positive number or +∞. Let us repeat the process for the right side.
f(x)=1/[(x-1)(x+2)]
f(-1.99)=1/((-1.99)-1)((-1.99)+2)]
f(-2.01)=1/[(-2.99)(0.01)]
f(-2.01)=-33.44 This is equivalent to a very large negative number.
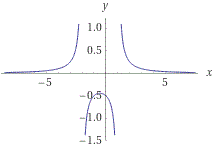
Therefore as x approaches the asymptote x=-2 from the right, the function approaches a very large negative number or -∞. Next we are to sketch a graph of the function. To graph the function remember the one sided limits for the vertical asymptotes. Draw the function such that it matches the one sided limits we just calculated.
f(-2.01)=1/((-2.01)-1)((-2.01)+2)]
f(-2.01)=1/[(-3.01)(-0.01)]
f(-2.01)=33.22 This is equivalent to a very large positive number. A number closer to 2 would have given us a larger number.
Therefore as x approaches the asymptote x=-2 from the left, the function approaches a very large positive number or +∞. Let us repeat the process for the right side.
f(x)=1/[(x-1)(x+2)]
f(-1.99)=1/((-1.99)-1)((-1.99)+2)]
f(-2.01)=1/[(-2.99)(0.01)]
f(-2.01)=-33.44 This is equivalent to a very large negative number.
Therefore as x approaches the asymptote x=-2 from the right, the function approaches a very large negative number or -∞. Next we are to sketch a graph of the function. To graph the function remember the one sided limits for the vertical asymptotes. Draw the function such that it matches the one sided limits we just calculated.
We can utilize what we have learned in the previous lessons on rational functions. Let's run though a problem where will solve for intervals of increase and decrease and where we will look at the concavity of the function.
For the following function, determine the intervals of increase and decrease. Then determine any points of inflection. Explain why the function never crosses the x-axis and why there are no vertical asymptotes. Last of all graph the function.
For the following function, determine the intervals of increase and decrease. Then determine any points of inflection. Explain why the function never crosses the x-axis and why there are no vertical asymptotes. Last of all graph the function.
To determine the intervals of increase and decrease, simply take the first derivative of the function and determine over what intervals the first derivative is positive or negative.
f(x)=1/[x²+4]
f(x)=(x²+4)^(-1)
f'(x)=(-1)[(x²+4)^(-2)](2x)
f'(x)=-2x/[(x²+4)^(2)]
To determine over what intervals f'(x) is increasing or decreasing solve f'(x)=0. Solve for f'(x):
0=-2x/[(x²+4)^(2)]
0=-2x
x=0
Therefore we have two intervals to check for:
Interval 1: x<0
Interval 2: x>0
For Interval 1 let us check x=-1:
f'(x)=-2x/[(x²+4)^(2)]
f'(-1)=-2(-1)/[((-1)²+4)^(2)]
f'(-1)=2/[(5)^(2)]
f'(-1)=2/25
For Interval 2 let us check x=1:
f'(x)=-2x/[(x²+4)^(2)]
f'(1)=-2(1)/[((1)²+4)^(2)]
f'(1)=-2/[(5)^(2)]
f'(1)=-2/25
Therefore f(x) is increasing over the interval x<0 and decreasing over the interval x>0. Next let us determine any points of inflection. To do this, take the second derivative, equate with zero, and solve. a point of inflection occurs when f''(x)=0 and when f''(x) switches sign on either side of the point of inflection. Let us begin.
f'(x)=-2x/[(x²+4)^(2)]
f'(x)=(-2x)[(x²+4)^(-2)]
f''(x)=d/dx(-2x)[(x²+4)^(-2)]+(-2x)d/dx[(x²+4)^(-2)]
f''(x)=(-2)[(x²+4)^(-2)]+(-2x)(-2)[(x²+4)^(-3)](2x)
f''(x)=(-2)[(x²+4)^(-2)]+8x²[(x²+4)^(-3)] Factor out the greatest common factor which is [(x²+4)^(-3)].
f''(x)=[(x²+4)^(-3)][(-2)(x²+4)+8x²]
f''(x)=[(x²+4)^(-3)][-2x²-8+8x²]
f''(x)=[(x²+4)^(-3)][6x²-8]
f''(x)=[6x²-8]/[(x²+4)^(3)]
Next solve f''(x)=0:
f''(x)=[6x²-8]/[(x²+4)^(3)]
0=[6x²-8]/[(x²+4)^(3)] Zero is equal to the numerator because 0 times the denominator is equal to 0.
0=[6x²-8]
0=6x²-8
8=6x²
8/6=x²
x²=4/3
x=±2/√3
Let us verify if this is a point of inflection by check to see if the sign of f''(x) changes across adjacent intervals. Note that we have three intervals to verify:
Interval 1: x<-2/√3
Interval 2: -2/√3<x<2/√3
Interval 3: x>2/√3
Now determine the sign of f''(x) for each of these three intervals.
For Interval 1 we choose to check x=-2 (note that -2/√3=-1.15 so we need a value that is less than this):
f''(x)=[6x²-8]/[(x²+4)^(3)]
f''(-2)=[6(-2)²-8]/[((-2)²+4)^(3)]
f''(-2)=(24-8)/(8^(3))
f''(-2)=(16)/(512)
f''(-2)=1/32 This result is concave up.
For Interval 2 let us check x=0:
f''(x)=[6x²-8]/[(x²+4)^(3)]
f''(0)=[6(0)²-8]/[((0)²+4)^(3)]
f''(0)=[-8]/[(4)^(3)]
f''(0)=[-8]/[64]
f''(0)=-1/8 This result is concave down.
For Interval 3 let us check x=2:
f''(x)=[6x²-8]/[(x²+4)^(3)]
f''(2)=[6(2)²-8]/[((2)²+4)^(3)]
f''(0)=[16]/[(8)^(3)]
f''(0)=(16)/(512)
f''(0)=1/32 This result is concave up.
The second derivative is positive over Interval 1 and 3 and negative over interval 2. Therefore we have a point of inflection between Interval 1 and 2 and another point of inflection between interval 2 and 3. Determine the full co-ordinates of the two points of inflection. We know that they occur at x=±2/√3.
f(x)=1/[x²+4]
f(2/√3)=1/[(2/√3)²+4]
f(2/√3)=1/(4/3+4)
f(2/√3)=1/(4/3+12/3)
f(2/√3)=1/(16/3)
f(2/√3)=3/16
f(x)=1/[x²+4]
f(-2/√3)=1/[(-2/√3)²+4]
f(-2/√3)=1/(4/3+4)
f(-2/√3)=1/(4/3+12/3)
f(-2/√3)=1/(16/3)
f(-2/√3)=3/16
Explain why the function never crosses the x-axis and why there are no vertical asymptotes. Last of all graph the function.
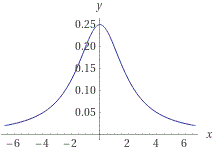
Therefore the two points of inflection are (2/√3, 3/16) and (-2/√3, 3/16). The function never crosses the x-axis because the denominator is a quadratic that has been translated upward. Therefore the denominator, x²+4, is never equal to zero. It is always greater than zero. Since the numerator is 1, the function itself always has a value greater than zero. Therefore it never crosses the x-axis. There are no vertical asymptotes because the denominator is never equal to zero. A vertical asymptote occurs where the denominator of a rational function is equated to zero and solved for. This is because a value of zero in the denominator is undefined. But since the denominator is always positive, a value of zero in the denominator is impossible and no vertical asymptote exists. To graph the function, we will note that the graph is concave up over x<-2/√3 and over x>2/√3. The graph is concave down over -2/√3<x<2/√3. This tells us that the graph is concave up over a large portion. We already know that the graph does not touch the x-axis and that there are two points of inflection at (2/√3, 3/16) and (-2/√3, 3/16). Determine the y-intercept so that we have three points and then draw a smooth curve through the points.
f(x)=1/[x²+4]
f(0)=1/[(0)²+4]
f(0)=1/4
Draw a smooth curve through (0, 1/4) and through the points of inflection at (2/√3, 3/16) and (-2/√3, 3/16).
f(x)=1/[x²+4]
f(x)=(x²+4)^(-1)
f'(x)=(-1)[(x²+4)^(-2)](2x)
f'(x)=-2x/[(x²+4)^(2)]
To determine over what intervals f'(x) is increasing or decreasing solve f'(x)=0. Solve for f'(x):
0=-2x/[(x²+4)^(2)]
0=-2x
x=0
Therefore we have two intervals to check for:
Interval 1: x<0
Interval 2: x>0
For Interval 1 let us check x=-1:
f'(x)=-2x/[(x²+4)^(2)]
f'(-1)=-2(-1)/[((-1)²+4)^(2)]
f'(-1)=2/[(5)^(2)]
f'(-1)=2/25
For Interval 2 let us check x=1:
f'(x)=-2x/[(x²+4)^(2)]
f'(1)=-2(1)/[((1)²+4)^(2)]
f'(1)=-2/[(5)^(2)]
f'(1)=-2/25
Therefore f(x) is increasing over the interval x<0 and decreasing over the interval x>0. Next let us determine any points of inflection. To do this, take the second derivative, equate with zero, and solve. a point of inflection occurs when f''(x)=0 and when f''(x) switches sign on either side of the point of inflection. Let us begin.
f'(x)=-2x/[(x²+4)^(2)]
f'(x)=(-2x)[(x²+4)^(-2)]
f''(x)=d/dx(-2x)[(x²+4)^(-2)]+(-2x)d/dx[(x²+4)^(-2)]
f''(x)=(-2)[(x²+4)^(-2)]+(-2x)(-2)[(x²+4)^(-3)](2x)
f''(x)=(-2)[(x²+4)^(-2)]+8x²[(x²+4)^(-3)] Factor out the greatest common factor which is [(x²+4)^(-3)].
f''(x)=[(x²+4)^(-3)][(-2)(x²+4)+8x²]
f''(x)=[(x²+4)^(-3)][-2x²-8+8x²]
f''(x)=[(x²+4)^(-3)][6x²-8]
f''(x)=[6x²-8]/[(x²+4)^(3)]
Next solve f''(x)=0:
f''(x)=[6x²-8]/[(x²+4)^(3)]
0=[6x²-8]/[(x²+4)^(3)] Zero is equal to the numerator because 0 times the denominator is equal to 0.
0=[6x²-8]
0=6x²-8
8=6x²
8/6=x²
x²=4/3
x=±2/√3
Let us verify if this is a point of inflection by check to see if the sign of f''(x) changes across adjacent intervals. Note that we have three intervals to verify:
Interval 1: x<-2/√3
Interval 2: -2/√3<x<2/√3
Interval 3: x>2/√3
Now determine the sign of f''(x) for each of these three intervals.
For Interval 1 we choose to check x=-2 (note that -2/√3=-1.15 so we need a value that is less than this):
f''(x)=[6x²-8]/[(x²+4)^(3)]
f''(-2)=[6(-2)²-8]/[((-2)²+4)^(3)]
f''(-2)=(24-8)/(8^(3))
f''(-2)=(16)/(512)
f''(-2)=1/32 This result is concave up.
For Interval 2 let us check x=0:
f''(x)=[6x²-8]/[(x²+4)^(3)]
f''(0)=[6(0)²-8]/[((0)²+4)^(3)]
f''(0)=[-8]/[(4)^(3)]
f''(0)=[-8]/[64]
f''(0)=-1/8 This result is concave down.
For Interval 3 let us check x=2:
f''(x)=[6x²-8]/[(x²+4)^(3)]
f''(2)=[6(2)²-8]/[((2)²+4)^(3)]
f''(0)=[16]/[(8)^(3)]
f''(0)=(16)/(512)
f''(0)=1/32 This result is concave up.
The second derivative is positive over Interval 1 and 3 and negative over interval 2. Therefore we have a point of inflection between Interval 1 and 2 and another point of inflection between interval 2 and 3. Determine the full co-ordinates of the two points of inflection. We know that they occur at x=±2/√3.
f(x)=1/[x²+4]
f(2/√3)=1/[(2/√3)²+4]
f(2/√3)=1/(4/3+4)
f(2/√3)=1/(4/3+12/3)
f(2/√3)=1/(16/3)
f(2/√3)=3/16
f(x)=1/[x²+4]
f(-2/√3)=1/[(-2/√3)²+4]
f(-2/√3)=1/(4/3+4)
f(-2/√3)=1/(4/3+12/3)
f(-2/√3)=1/(16/3)
f(-2/√3)=3/16
Explain why the function never crosses the x-axis and why there are no vertical asymptotes. Last of all graph the function.
Therefore the two points of inflection are (2/√3, 3/16) and (-2/√3, 3/16). The function never crosses the x-axis because the denominator is a quadratic that has been translated upward. Therefore the denominator, x²+4, is never equal to zero. It is always greater than zero. Since the numerator is 1, the function itself always has a value greater than zero. Therefore it never crosses the x-axis. There are no vertical asymptotes because the denominator is never equal to zero. A vertical asymptote occurs where the denominator of a rational function is equated to zero and solved for. This is because a value of zero in the denominator is undefined. But since the denominator is always positive, a value of zero in the denominator is impossible and no vertical asymptote exists. To graph the function, we will note that the graph is concave up over x<-2/√3 and over x>2/√3. The graph is concave down over -2/√3<x<2/√3. This tells us that the graph is concave up over a large portion. We already know that the graph does not touch the x-axis and that there are two points of inflection at (2/√3, 3/16) and (-2/√3, 3/16). Determine the y-intercept so that we have three points and then draw a smooth curve through the points.
f(x)=1/[x²+4]
f(0)=1/[(0)²+4]
f(0)=1/4
Draw a smooth curve through (0, 1/4) and through the points of inflection at (2/√3, 3/16) and (-2/√3, 3/16).
Note that it is important to check concavity around a vertical asymptote as there may be no point of inflection but a change in concavity, or a change in the sign of f''(x) may occur. Let us go though a sample problem.
Find the intervals of concavity for the following function. Then graph the function.
Find the intervals of concavity for the following function. Then graph the function.
In order to determine the intervals of concavity we need the second derivative.
f(x)=-1/(x-1)
f(x)=-1(x-1)^(-1)
f'(x)=-1(-1)(x-1)^(-2)
f'(x)=(x-1)^(-2)
f''(x)=-2(x-1)^(-3)
f''(x)=-2/(x-1)^(3)
We note that we have a number in the numerator not a variable. If we set f''(x) to zero we would get no results for x:
0=-2/(x-1)^(3) Multiply the denominator by 0.
0≠2 We do not get a result for x.
This tells us that there exists no inflection points. However, we know that there exists the same vertical asymptote, x=1, in f''(x) as in the original function. We can check the intervals of concavity around this vertical asymptote. We can create two intervals and then we can check to see if the sign of f''(x) changes.
Interval 1: x<1
Interval 2: x>1
For Interval 1 check x=0:
f''(x)=-2/(x-1)^(3)
f''(0)=-2/((0)-1)^(3)
f''(0)=-2/-1
f''(0)=2
For Interval 2 check x=2:
f''(x)=-2/(x-1)^(3)
f''(2)=-2/((2)-1)^(3)
f''(2)=-2/1
f''(2)=-2
Therefore f''(x) changes signs at the vertical asymptote x=1. For Interval 1, x<1, the function is concave up because f''(x) is positive. For Interval 2, x>1, the function is concave down because f''(x) is negative. Based on concavity, we can draw our graph. Note that left of the vertical asymptote the graph opens upward because the function is concave up and to the right of it the function opens downward because it is concave down.
f(x)=-1/(x-1)
f(x)=-1(x-1)^(-1)
f'(x)=-1(-1)(x-1)^(-2)
f'(x)=(x-1)^(-2)
f''(x)=-2(x-1)^(-3)
f''(x)=-2/(x-1)^(3)
We note that we have a number in the numerator not a variable. If we set f''(x) to zero we would get no results for x:
0=-2/(x-1)^(3) Multiply the denominator by 0.
0≠2 We do not get a result for x.
This tells us that there exists no inflection points. However, we know that there exists the same vertical asymptote, x=1, in f''(x) as in the original function. We can check the intervals of concavity around this vertical asymptote. We can create two intervals and then we can check to see if the sign of f''(x) changes.
Interval 1: x<1
Interval 2: x>1
For Interval 1 check x=0:
f''(x)=-2/(x-1)^(3)
f''(0)=-2/((0)-1)^(3)
f''(0)=-2/-1
f''(0)=2
For Interval 2 check x=2:
f''(x)=-2/(x-1)^(3)
f''(2)=-2/((2)-1)^(3)
f''(2)=-2/1
f''(2)=-2
Therefore f''(x) changes signs at the vertical asymptote x=1. For Interval 1, x<1, the function is concave up because f''(x) is positive. For Interval 2, x>1, the function is concave down because f''(x) is negative. Based on concavity, we can draw our graph. Note that left of the vertical asymptote the graph opens upward because the function is concave up and to the right of it the function opens downward because it is concave down.
That's all there is to this lesson. Simply remember that just because no inflection point exists does not mean that intervals of concavity do not exist. They still need to be verified even if a vertical asymptote is what separates the intervals of concavity.
© 2020 MyMathEducator.com All Rights Reserved.