Sentry Page Protection
Please Wait...
Lesson 16: Applying Everything
We have learned to do a lot with the first derivative and the second derivative of a function. With these we can identify critical points, determine intervals of increase and decrease, and determine intervals of concavity. In this lesson, we will be using everything we learned up to now to graph functions. Before we proceed with a problem, let us remember what an odd function is and what an even function is:
We begin by checking to see if the function is odd or even. Determine f(-x) and f(-x) so that we can compare them with f(x).
f(x)=x³+3x²+3x
f(-x)=(-x)³+3(-x)²+3(-x)
f(-x)=-x³+3x²-3x
-f(x)=-[x³+3x²+3x]
-f(x)=-x³-3x²-3x
Therefore the function is neither odd or even. The function is defined over all real values of x because there exist no restrictions on the values that x can take on so the domain of f(x) is {x:xεR}. Next we must determine all intercepts:
For the y-intercept (let x=0):
f(x)=x³+3x²+3x
f(0)=(0)³+3(0)²+3(0)
f(0)=0
For the x-intercept (let y=0):
f(x)=x³+3x²+3x
0=x³+3x²+3x
0=x(x²+3x+3)
x=0 or x=[-3±√(3)²-4(1)(3)]/2a Here we use the quadratic formula to check if there is a solution. There is not because √-3 is undefined.
x=0
Therefore the only intercept is (0,0). Next we must determine all critical points and classify them. To do this take the first and second derivative and equate with 0.
f(x)=x³+3x²+3x
f'(x)=3x²+6x+3
0=3x²+6x+3
0=3x²+3x+3x+3
0=3x(x+1)+3(x+1)
0=3x(x+1)+3(x+1)
0=(3x+3)(x+1)
3x+3=0 or x+1=0
x=-3/3 or x=-1
x=-1
f'(x)=3x²+6x+3
f''(x)=6x+6
0=6x+6
x=-6/6
x=-1
Therefore we have one critical number at x=-1. Before we classify it let us look at intervals of increase and decrease and intervals of concavity. Our only critical number, x=-1, creates two intervals. Interval 1 is x<-1 and Interval 2 is x>-1. Let us take test values in each interval:
For Interval 1 (test x=-2):
f'(x)=3x²+6x+3
f'(-2)=3(-2)²+6(-2)+3
f'(-2)=12-12+3
f'(-2)=3
f''(x)=6x+6
f''(-2)=6(-2)+6
f''(-2)=-12+6
f''(-2)=-6
Because the first derivative is positive and because the second derivative is negative over x<-1, the function f(x) is increasing and is concave down over the interval x<-1. Let us repeat the process for the interval x>-1:
For Interval 2 (test x=1):
f'(x)=3x²+6x+3
f'(1)=3(1)²+6(1)+3
f'(1)=3+6+3
f'(1)=12
f''(x)=6x+6
f''(1)=6(1)+6
f''(1)=12
Because the first and second derivative are positive over x>-1, the function f(x) is increasing and is concave up over the interval x>-1. Now let us take a look at x=-1. Earlier, we discovered that f''(-1)=0. Since the second derivative changes from negative to positive as x values increase past x=-1, we have a point of inflection. Substitute x=-1 into f(x) to determine the co-ordinates of the point of inflection.
f(x)=x³+3x²+3x
f(-1)=(-1)³+3(-1)²+3(-1)
f(-1)=-1+3-3
f(-1)=-1
Therefore (-1,-1) is the point of inflection. Next let us go through a problem where we have to sketch the graph. Before we do so, it is helpful to know that we can compile all the information we need to sketch a graph into a series of steps:
Step 1: Determine the domain of the function.
Step 2: Determine all intercepts of the function.
Step 3: Determine and classify all critical numbers of the function.
Step 4: Determine all the points of inflection.
Step 5: Determine the intervals of increase and decrease and the intervals of concavity,
Step 6: Sketch the function.
Note that we have already gone over most of these steps in the last problem, but now we will be going over them with the intention of graphing our function. Let us dive into our problem.
For the following function analyze all of its key features. Then sketch its graph.
f(x)=x³+6x²+8x
Note that when we are told to analyze all key features, we are really being asked to follow the step by step analysis listed above. We begin by determining the domain of the function. Since there is no restriction on the values x can take on, the function is defined over all values of x. Therefore the domain is {x:xεR}. Next, let us proceed to Step 2, which consists of taking all intercepts of the function. We begin with the y-intercept:
f(x)=x³+6x²+8x
f(0)=(0)³+6(0)²+8(0)
f(0)=0
Therefore, the y-intercept occurs at (0,0), Now solve for the x-intercepts:
f(x)=x³+6x²+8x
0=x³+6x²+8x
0=x(x²+6x+8)
0=x(x+4)(x+2)
x=0 or x=-4 or x=-2
Therefore, the x-intercepts are (0,0), (-4,0), and (-2,0). The next step is to determine and classify all critical numbers of the function. Take the derivative, equate it with zero, and solve.
f(x)=x³+6x²+8x
f'(x)=3x²+12x+8
0=3x²+12x+8
Since the trinomial above cannot be factored, use the quadratic formula to determine all of the x-intercepts.
x=[-b±√b²-4ac]/2a a=3, b=12, and c=8
x=[-12±√((12)²-4(3)(8))]/2(3)
x=[-12±√48]/6
x=-0.84 or x=-3.15
Substitute the critical numbers into f(x) to get the co-ordinates.
f(x)=x³+6x²+8x
f(-0.84)=(-0.84)³+6(-0.84)²+8(-0.84)
f(-0.84)=(-0.84)³+6(-0.84)²+8(-0.84)
f(-0.84)=-0.593+4.234-6.72
f(-0.84)=-3.079
f(x)=x³+6x²+8x
f(-3.15)=(-3.15)³+6(-3.15)²+8(-3.15)
f(-3.15)=(-3.15)³+6(-3.15)²+8(-3.15)
f(-3.15)=-31.256+59.535-25.2
f(-3.15)=-31.256+59.535-25.2
f(-3.15)=3.079
Therefore the critical numbers are (-0.84,-3.08) and (-3.15,3.08). To find and classify critical numbers, utilize the second derivative test. Substitute each value into the second derivative and check and see if your result is positive or negative.
f'(x)=3x²+12x+8 Take the derivative of the second derivative.
f''(x)=6x+12
f''(-0.84)=6(-0.84)+12
f''(-0.84)=-5.04+12
f''(-0.84)=6.96
f''(-3.15)=6(-3.15)+12
f''(-3.15)=-18.9+12
f''(-3.15)=-6.9
Because the second derivative is positive at x=-0.84, (-0.84,-3.08) is a local minimum. Likewise, because the second derivative is negative at x=-3.15, (-3.15,3.08) is a local maximum. The next step is to determine all points of inflection. To do this take the second derivative, equate it with zero, and solve.
f''(x)=6x+12
0=6x+12
-12=6x
x=-2
To make sure this is a point of inflection we must check to see if the concavity of the function changes around this point. Verify for test values on either side of x=-2:
f''(x)=6x+12
f''(-3)=6(-3)+12
f''(-3)=-18+12
f''(-3)=-6
f''(x)=6x+12
f''(0)=6(0)+12
f''(0)=12
Since the second derivative changes signs there exists a point of inflection at x=-2. Determine the y-coordinate.
f(x)=x³+6x²+8x
f(-2)=(-2)³+6(-2)²+8(-2)
f(-2)=-8+24-16
f(-2)=0
Therefore the point of inflection occurs at (-2,0). The next step is to determine the intervals of increase and decrease and the intervals of concavity. First, let us create our intervals based on the maxima, minima, and the point of inflection. We have a local maximum at -3.15, a point of inflection at -2, and a local minimum at -0.84. This means we have four intervals:
Interval 1: x<-3.15
Interval 2: -3.15<x<-2
Interval 3: -2<x<-0.84
Interval 4: x>-0.84
For each interval, test a value within the first and second derivative and summarize the results.
For Interval 1 (test x=-4):
f'(x)=3x²+12x+8
f'(-4)=3(-4)²+12(-4)+8
f'(-4)=48-48+8
f'(-4)=8
f''(x)=6x+12
f''(-4)=6(-4)+12
f''(-4)=-12
Because the first derivative is positive over the interval x<-3.15, the function is increasing over this interval. Also, because the second derivative is negative, the function is concave down over this interval. Let us test the next interval:
For Interval 2 (test x=-3):
f'(x)=3x²+12x+8
f'(-3)=3(-3)²+12(-3)+8
f'(-3)=27-36+8
f'(-3)=-1
f''(x)=6x+12
f''(-3)=6(-3)+12
f''(-3)=-6
Since the first derivative is negative over the interval -3.15<x<-2, the function is decreasing over this interval. Also, because the second derivative is negative, the function is concave down over the interval -3.15<x<-2.
For Interval 3 (test x=-1):
f'(x)=3x²+12x+8
f'(-1)=3(-1)²+12(-1)+8
f'(-1)=3-12+8
f'(-1)=-1
f''(x)=6x+12
f''(-1)=6(-1)+12
f''(-1)=6
Since the first derivative is negative over the interval -2<x<-0.84, the function is decreasing over this interval. In addition, because the second derivative of the original function is positive, the original function is concave up over the interval -2<x<-0.84. Let's repeat for the last interval.
For Interval 4 (test x=1):
f'(x)=3x²+12x+8
f'(1)=3(1)²+12(1)+8
f'(1)=3+12+8
f'(1)=23
f''(x)=6x+12
f''(1)=6(1)+12
f''(1)=18
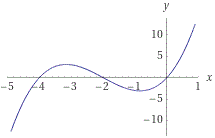
Because the first derivative is positive over the interval x>-0.84, the function is increasing over this interval. Also, because the second derivative is positive over the interval, the function is concave up over the interval x>-0.84. The last step is to sketch the function. Remember, all key points and draw a smooth curve through them. The function has intercepts at (0,0), (-4,0), and (-2,0). Also, the function has a local minimum at (-0.84,-3.08) and a local maximum at (-3.15,3.08). Finally, we also note that the function has a point of inflection at (-2,0), To sketch the function simply draw a smooth curve through all of these points.
- An even function, f(x), is symmetrical about the y-axis for all values of x. That is, f(x)=f(-x) for all values of x.
- An odd function, f(x), is symmetrical about the origin. This means that f(-x)=-f(x) for all values of x.
We begin by checking to see if the function is odd or even. Determine f(-x) and f(-x) so that we can compare them with f(x).
f(x)=x³+3x²+3x
f(-x)=(-x)³+3(-x)²+3(-x)
f(-x)=-x³+3x²-3x
-f(x)=-[x³+3x²+3x]
-f(x)=-x³-3x²-3x
Therefore the function is neither odd or even. The function is defined over all real values of x because there exist no restrictions on the values that x can take on so the domain of f(x) is {x:xεR}. Next we must determine all intercepts:
For the y-intercept (let x=0):
f(x)=x³+3x²+3x
f(0)=(0)³+3(0)²+3(0)
f(0)=0
For the x-intercept (let y=0):
f(x)=x³+3x²+3x
0=x³+3x²+3x
0=x(x²+3x+3)
x=0 or x=[-3±√(3)²-4(1)(3)]/2a Here we use the quadratic formula to check if there is a solution. There is not because √-3 is undefined.
x=0
Therefore the only intercept is (0,0). Next we must determine all critical points and classify them. To do this take the first and second derivative and equate with 0.
f(x)=x³+3x²+3x
f'(x)=3x²+6x+3
0=3x²+6x+3
0=3x²+3x+3x+3
0=3x(x+1)+3(x+1)
0=3x(x+1)+3(x+1)
0=(3x+3)(x+1)
3x+3=0 or x+1=0
x=-3/3 or x=-1
x=-1
f'(x)=3x²+6x+3
f''(x)=6x+6
0=6x+6
x=-6/6
x=-1
Therefore we have one critical number at x=-1. Before we classify it let us look at intervals of increase and decrease and intervals of concavity. Our only critical number, x=-1, creates two intervals. Interval 1 is x<-1 and Interval 2 is x>-1. Let us take test values in each interval:
For Interval 1 (test x=-2):
f'(x)=3x²+6x+3
f'(-2)=3(-2)²+6(-2)+3
f'(-2)=12-12+3
f'(-2)=3
f''(x)=6x+6
f''(-2)=6(-2)+6
f''(-2)=-12+6
f''(-2)=-6
Because the first derivative is positive and because the second derivative is negative over x<-1, the function f(x) is increasing and is concave down over the interval x<-1. Let us repeat the process for the interval x>-1:
For Interval 2 (test x=1):
f'(x)=3x²+6x+3
f'(1)=3(1)²+6(1)+3
f'(1)=3+6+3
f'(1)=12
f''(x)=6x+6
f''(1)=6(1)+6
f''(1)=12
Because the first and second derivative are positive over x>-1, the function f(x) is increasing and is concave up over the interval x>-1. Now let us take a look at x=-1. Earlier, we discovered that f''(-1)=0. Since the second derivative changes from negative to positive as x values increase past x=-1, we have a point of inflection. Substitute x=-1 into f(x) to determine the co-ordinates of the point of inflection.
f(x)=x³+3x²+3x
f(-1)=(-1)³+3(-1)²+3(-1)
f(-1)=-1+3-3
f(-1)=-1
Therefore (-1,-1) is the point of inflection. Next let us go through a problem where we have to sketch the graph. Before we do so, it is helpful to know that we can compile all the information we need to sketch a graph into a series of steps:
Step 1: Determine the domain of the function.
Step 2: Determine all intercepts of the function.
Step 3: Determine and classify all critical numbers of the function.
Step 4: Determine all the points of inflection.
Step 5: Determine the intervals of increase and decrease and the intervals of concavity,
Step 6: Sketch the function.
Note that we have already gone over most of these steps in the last problem, but now we will be going over them with the intention of graphing our function. Let us dive into our problem.
For the following function analyze all of its key features. Then sketch its graph.
f(x)=x³+6x²+8x
Note that when we are told to analyze all key features, we are really being asked to follow the step by step analysis listed above. We begin by determining the domain of the function. Since there is no restriction on the values x can take on, the function is defined over all values of x. Therefore the domain is {x:xεR}. Next, let us proceed to Step 2, which consists of taking all intercepts of the function. We begin with the y-intercept:
f(x)=x³+6x²+8x
f(0)=(0)³+6(0)²+8(0)
f(0)=0
Therefore, the y-intercept occurs at (0,0), Now solve for the x-intercepts:
f(x)=x³+6x²+8x
0=x³+6x²+8x
0=x(x²+6x+8)
0=x(x+4)(x+2)
x=0 or x=-4 or x=-2
Therefore, the x-intercepts are (0,0), (-4,0), and (-2,0). The next step is to determine and classify all critical numbers of the function. Take the derivative, equate it with zero, and solve.
f(x)=x³+6x²+8x
f'(x)=3x²+12x+8
0=3x²+12x+8
Since the trinomial above cannot be factored, use the quadratic formula to determine all of the x-intercepts.
x=[-b±√b²-4ac]/2a a=3, b=12, and c=8
x=[-12±√((12)²-4(3)(8))]/2(3)
x=[-12±√48]/6
x=-0.84 or x=-3.15
Substitute the critical numbers into f(x) to get the co-ordinates.
f(x)=x³+6x²+8x
f(-0.84)=(-0.84)³+6(-0.84)²+8(-0.84)
f(-0.84)=(-0.84)³+6(-0.84)²+8(-0.84)
f(-0.84)=-0.593+4.234-6.72
f(-0.84)=-3.079
f(x)=x³+6x²+8x
f(-3.15)=(-3.15)³+6(-3.15)²+8(-3.15)
f(-3.15)=(-3.15)³+6(-3.15)²+8(-3.15)
f(-3.15)=-31.256+59.535-25.2
f(-3.15)=-31.256+59.535-25.2
f(-3.15)=3.079
Therefore the critical numbers are (-0.84,-3.08) and (-3.15,3.08). To find and classify critical numbers, utilize the second derivative test. Substitute each value into the second derivative and check and see if your result is positive or negative.
f'(x)=3x²+12x+8 Take the derivative of the second derivative.
f''(x)=6x+12
f''(-0.84)=6(-0.84)+12
f''(-0.84)=-5.04+12
f''(-0.84)=6.96
f''(-3.15)=6(-3.15)+12
f''(-3.15)=-18.9+12
f''(-3.15)=-6.9
Because the second derivative is positive at x=-0.84, (-0.84,-3.08) is a local minimum. Likewise, because the second derivative is negative at x=-3.15, (-3.15,3.08) is a local maximum. The next step is to determine all points of inflection. To do this take the second derivative, equate it with zero, and solve.
f''(x)=6x+12
0=6x+12
-12=6x
x=-2
To make sure this is a point of inflection we must check to see if the concavity of the function changes around this point. Verify for test values on either side of x=-2:
f''(x)=6x+12
f''(-3)=6(-3)+12
f''(-3)=-18+12
f''(-3)=-6
f''(x)=6x+12
f''(0)=6(0)+12
f''(0)=12
Since the second derivative changes signs there exists a point of inflection at x=-2. Determine the y-coordinate.
f(x)=x³+6x²+8x
f(-2)=(-2)³+6(-2)²+8(-2)
f(-2)=-8+24-16
f(-2)=0
Therefore the point of inflection occurs at (-2,0). The next step is to determine the intervals of increase and decrease and the intervals of concavity. First, let us create our intervals based on the maxima, minima, and the point of inflection. We have a local maximum at -3.15, a point of inflection at -2, and a local minimum at -0.84. This means we have four intervals:
Interval 1: x<-3.15
Interval 2: -3.15<x<-2
Interval 3: -2<x<-0.84
Interval 4: x>-0.84
For each interval, test a value within the first and second derivative and summarize the results.
For Interval 1 (test x=-4):
f'(x)=3x²+12x+8
f'(-4)=3(-4)²+12(-4)+8
f'(-4)=48-48+8
f'(-4)=8
f''(x)=6x+12
f''(-4)=6(-4)+12
f''(-4)=-12
Because the first derivative is positive over the interval x<-3.15, the function is increasing over this interval. Also, because the second derivative is negative, the function is concave down over this interval. Let us test the next interval:
For Interval 2 (test x=-3):
f'(x)=3x²+12x+8
f'(-3)=3(-3)²+12(-3)+8
f'(-3)=27-36+8
f'(-3)=-1
f''(x)=6x+12
f''(-3)=6(-3)+12
f''(-3)=-6
Since the first derivative is negative over the interval -3.15<x<-2, the function is decreasing over this interval. Also, because the second derivative is negative, the function is concave down over the interval -3.15<x<-2.
For Interval 3 (test x=-1):
f'(x)=3x²+12x+8
f'(-1)=3(-1)²+12(-1)+8
f'(-1)=3-12+8
f'(-1)=-1
f''(x)=6x+12
f''(-1)=6(-1)+12
f''(-1)=6
Since the first derivative is negative over the interval -2<x<-0.84, the function is decreasing over this interval. In addition, because the second derivative of the original function is positive, the original function is concave up over the interval -2<x<-0.84. Let's repeat for the last interval.
For Interval 4 (test x=1):
f'(x)=3x²+12x+8
f'(1)=3(1)²+12(1)+8
f'(1)=3+12+8
f'(1)=23
f''(x)=6x+12
f''(1)=6(1)+12
f''(1)=18
Because the first derivative is positive over the interval x>-0.84, the function is increasing over this interval. Also, because the second derivative is positive over the interval, the function is concave up over the interval x>-0.84. The last step is to sketch the function. Remember, all key points and draw a smooth curve through them. The function has intercepts at (0,0), (-4,0), and (-2,0). Also, the function has a local minimum at (-0.84,-3.08) and a local maximum at (-3.15,3.08). Finally, we also note that the function has a point of inflection at (-2,0), To sketch the function simply draw a smooth curve through all of these points.
That's all there is to this lesson. Just remember that when you are asked to analyze the features of a function, you are being to follow the multiple step process that concludes in sketching the function. As part of the six step process, you must determine the domain of the function, the intercepts of the function, the critical numbers of the function, and all points of inflection. You are also required to determine the intervals of increase and decrease, as well as the intervals of concavity. Lastly, utilize all given information to sketch the function.
© 2020 MyMathEducator.com All Rights Reserved