Sentry Page Protection
Please Wait...
Lesson 14: Concavity and the Second Derivative Test
In this lesson, we will be analyzing how the slope of the tangent to a graph is increasing or decreasing. That is to say, we will be analyzing the rate of change of the slope of the tangent. This rate of change is expressed by the second derivative. Remember, the second derivative is the derivative of the first derivative and the first derivative allows us to determine if the original function is increasing or decreasing. Let us go over some terminology related to concavity:
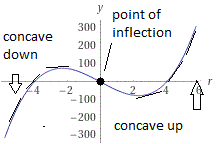
- The graph of f(x) is concave up over an interval a<x<b if all tangents to the curve over this interval are below the curve. The curve will loop upward over this interval and the second derivative, f''(x), will be positive over this interval because the rate of change of the tangent is increasing.
- The graph of f(x) is concave down over an interval a<x<b if all tangents to the curve over this interval are above the curve. The curve will loop downward over this interval and the second derivative, f''(x), will be negative over this interval because the rate of change of the tangent is decreasing.
- A point of inflection occurs when the graph changes from being concave up to being concave down, or from being concave down to being concave up. The second derivative, f''(x), is equal to zero at this point because the rate of change is going from decreasing to increasing, or vice versa.
Next, let us go over the second derivative test. The second derivative test allows us to classify critical points.
The Second Derivative Test
The Second Derivative Test
- If f'(a)=0, we know we have a critical point. If f'(a)=0 and f''(a)>0, then there exists a local minimum at (a,f(a)) and the curve is concave up. That is, if the second derivative is positive when the first derivative is zero, then we have a local minimum. This is because the slope of the tangent is increasing.
- If f'(a)=0 and f''(a)<0, then there exists a local maximum at (a,f(a)) and the curve is concave down. That is, if the second derivative is negative when the first derivative is positive, then we have a local maximum. This is because the slope of the tangent is decreasing.
- If f'(a)=0 and f''(a)=0 while f''(a) is changing signs at a, then we have a point of inflection at (a,f(a)). (Note that in rare cases f'(a) does not exist is a condition, along f''(a) for a point of inflection to exist). Also note that f''(a) must also equal to zero for a point of inflection to exist. That is if f'(a) alone is equal to zero, there is no point of inflection.
Let's run through a problem where we are required to locate all points of inflection and the intervals of concavity. In this type of problem we will limit ourselves to the second derivative test. Because a point of inflection occurs when f''(a) is changing signs, all we have to do is solve f(a)=0 to determine all inflection points. Then we can check our intervals to see if they are concave up or concave down. If the second derivative is positive, then the curve is concave up. If the second derivative is negative, then the curve is concave down. Let us begin.
For the function f(x)=x⁴-2x³-12x²+3x+2 determine all points of inflection and the intervals of concavity.
First find the second derivative. Then let it equal to zero and solve for the points of inflection.
f(x)=x⁴-2x³-12x²+3x+2
f'(x)=4x³-6x²-24x+3
f''(x)=12x²-12x-24 The derivative of the first derivative is the second derivative.
0=12x²-12x-24 Let the second derivative equal zero and solve.
0=12(x²-x-2)
0=x²-x-2
0=(x-2)(x+1)
x=2 or x=-1
From the zeros, we can create three intervals for testing:
Interval 1: x<-1
Interval 2: -1<x<2
Interval 3: x>2
Choose an arbitrary point in each interval and substitute into f''(x) to determine if that interval is concave up or concave down.
For Interval 1: x<-1
Choose x=-2.
f''(x)=12x²-12x-24
f''(-2)=12(-2)²-12(-2)-24
f''(-2)=48+24-24
f''(-2)=48 This interval is concave up since f''(-2)>0.
For Interval 2: -1<x<2
Choose x=0.
f''(x)=12x²-12x-24
f''(0)=12(0)²-12(0)-24
f''(0)=-24 This interval is concave down since f''(0)<0.
For Interval 3: x>2
Choose x=3.
f''(x)=12x²-12x-24
f''(3)=12(3)²-12(3)-24
f''(3)=108-36-24
f''(3)=48 This interval is concave up since f''(3)>0.
Last of all determine the co-ordinates of the points of inflection by substituting x=-1 and x=2 into the original function, f(x):
f(x)=x⁴-2x³-12x²+3x+2
f(-1)=(-1)⁴-2(-1)³-12(-1)²+3(-1)+2
f(-1)=1+2-12-3+2
f(-1)=-10
f(x)=x⁴-2x³-12x²+3x+2
f(2)=(2)⁴-2(2)³-12(2)²+3(2)+2
f(2)=16-16-48+6+2
f(2)=-40
There are three intervals of concavity. The function, f(x)=x⁴-2x³-12x²+3x+2, is concave up over the intervals x<-1 and x>2. The function is also concave down over the interval -1<x<2. The points of inflection separating these intervals are (-1,-10) and (2,-40). Note that there is also another method to solve this type of problem which involves taking the graph of the second derivative. The zeros will be the points of inflection and the graph will reveal where the original function is concave up or down based on where the second derivative is positive or negative. In other words we will have to graph the second derivative. We already took the zeros of the second derivative:
f''(x)=12x²-12x-24 This is the same work from above.
0=12x²-12x-24
0=12(x²-x-2)
0=x²-x-2
0=(x-2)(x+1)
x=2 or x=-1
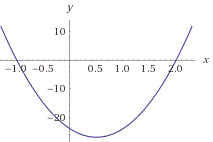
Therefore the x-intercepts are (2,0) and (-1,0). Let us also get the y-intercept so we can have three points to graph f''(x):
f''(0)=12(0)²-12(0)-24 Solve f''(0) to get the y-intercept.
f''(0)=-24
Therefore the y-intercept is (0,-24) and the x-intercepts are (2,0) and (-1,0). Graph the function.
For the function f(x)=x⁴-2x³-12x²+3x+2 determine all points of inflection and the intervals of concavity.
First find the second derivative. Then let it equal to zero and solve for the points of inflection.
f(x)=x⁴-2x³-12x²+3x+2
f'(x)=4x³-6x²-24x+3
f''(x)=12x²-12x-24 The derivative of the first derivative is the second derivative.
0=12x²-12x-24 Let the second derivative equal zero and solve.
0=12(x²-x-2)
0=x²-x-2
0=(x-2)(x+1)
x=2 or x=-1
From the zeros, we can create three intervals for testing:
Interval 1: x<-1
Interval 2: -1<x<2
Interval 3: x>2
Choose an arbitrary point in each interval and substitute into f''(x) to determine if that interval is concave up or concave down.
For Interval 1: x<-1
Choose x=-2.
f''(x)=12x²-12x-24
f''(-2)=12(-2)²-12(-2)-24
f''(-2)=48+24-24
f''(-2)=48 This interval is concave up since f''(-2)>0.
For Interval 2: -1<x<2
Choose x=0.
f''(x)=12x²-12x-24
f''(0)=12(0)²-12(0)-24
f''(0)=-24 This interval is concave down since f''(0)<0.
For Interval 3: x>2
Choose x=3.
f''(x)=12x²-12x-24
f''(3)=12(3)²-12(3)-24
f''(3)=108-36-24
f''(3)=48 This interval is concave up since f''(3)>0.
Last of all determine the co-ordinates of the points of inflection by substituting x=-1 and x=2 into the original function, f(x):
f(x)=x⁴-2x³-12x²+3x+2
f(-1)=(-1)⁴-2(-1)³-12(-1)²+3(-1)+2
f(-1)=1+2-12-3+2
f(-1)=-10
f(x)=x⁴-2x³-12x²+3x+2
f(2)=(2)⁴-2(2)³-12(2)²+3(2)+2
f(2)=16-16-48+6+2
f(2)=-40
There are three intervals of concavity. The function, f(x)=x⁴-2x³-12x²+3x+2, is concave up over the intervals x<-1 and x>2. The function is also concave down over the interval -1<x<2. The points of inflection separating these intervals are (-1,-10) and (2,-40). Note that there is also another method to solve this type of problem which involves taking the graph of the second derivative. The zeros will be the points of inflection and the graph will reveal where the original function is concave up or down based on where the second derivative is positive or negative. In other words we will have to graph the second derivative. We already took the zeros of the second derivative:
f''(x)=12x²-12x-24 This is the same work from above.
0=12x²-12x-24
0=12(x²-x-2)
0=x²-x-2
0=(x-2)(x+1)
x=2 or x=-1
Therefore the x-intercepts are (2,0) and (-1,0). Let us also get the y-intercept so we can have three points to graph f''(x):
f''(0)=12(0)²-12(0)-24 Solve f''(0) to get the y-intercept.
f''(0)=-24
Therefore the y-intercept is (0,-24) and the x-intercepts are (2,0) and (-1,0). Graph the function.
From the graph we see that f''(x) is positive when x<-1 and when x>2. We also see from the graph that f''(x) is negative over the interval -1<x<2. As a result, we can summarize that over the intervals x<-1 and x>2, the function f(x) is concave up. Also, the function is concave down over the interval -1<x<2. By looking at the graph further we see that f''(x) changes sign at x=-1 and at x=2. This leads us to conclude that x=-1 and x=2 are inflection points. To determine their co-ordinates, we substitute into f(x):
f(x)=x⁴-2x³-12x²+3x+2
f(-1)=(-1)⁴-2(-1)³-12(-1)²+3(-1)+2
f(-1)=1+2-12-3+2
f(-1)=-10
f(x)=x⁴-2x³-12x²+3x+2
f(2)=(2)⁴-2(2)³-12(2)²+3(2)+2
f(2)=16-16-48+6+2
f(2)=-40
Therefore the function f(x)=x⁴-2x³-12x²+3x+2 has two inflection points located at (-1,10) and at (2,-40). Next, let's go through a problem where we are asked to locate local maxima and minima. When we are asked to use the second derivative test along with the critical points the problem is only concerned with the classification of the critical points. The points can be a local maximum or minimum. Note that the problem is not concerned with the intervals of concavity, as the last type of problem was.
For the following function, find the critical points. Use the second derivative test for classification.
f(x)=x³-9x²+3
The first step is to determine the critical numbers for f(x). Remember, the critical numbers are found by taking the first derivative, letting it equal zero, and solving.
f(x)=x³-9x²+3
f'(x)=3x²-18x
0=3x²-18x Let the first derivative equal zero and solve.
0=3x(x-6)
3x=0 or x-6=0
x=0 or x=6 These are our critical numbers.
Substitute our critical numbers into our original function to get our critical points. Then we can analyze using the second derivative test.
f(x)=x³-9x²+3
f(0)=(0)³-9(0)²+3
f(0)=3
f(x)=x³-9x²+3
f(6)=(6)³-9(6)²+3
f(6)=216-324+3
f(6)=-105
Now let us check these points using the second derivate test. First, we take the second derivative of f(x). Then we substitute these points into the second derivative. If the critical number yields a negative result in the second derivative test, then the curve is concave down at that point. Likewise, if the critical number yields a positive result in the second derivative test, then the curve is concave up at that point. Let us run the second derivative test on our two points.
f'(x)=3x²-18x
f''(x)=6x-18
f''(x)=6x-18
f''(0)=6(0)-18
f''(0)=-18 The curve is concave down at this point because the result is negative.
f''(x)=6x-18
f''(6)=6(6)-18
f''(6)=18 The curve is concave up at this point because the result is positive.
Note that because x=0 and x=6 are critical numbers, such that f'(0) and f'(6) are equal to zero, they constitute local maxima and minima. Since the point (0,3) lies on a curve that is concave down, it is a local maximum. Also, since the point (6,-105) lies on a curve that is concave up, it is a local minimum. Let us go through one last type of problem where we are given a set of conditions and asked to graph the function that meets all of the conditions. Note that numerous graphs are possible but you must identify the critical points and draw them on the graph to meet the conditions.
Sketch a function that satisfies all of the following conditions.
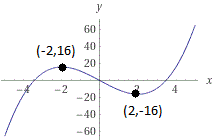
f''(x)<0 when x<0, f''(x)>0 when x>0, f'(-2)=0, f(-2)=16, f'(2)=0, f'(2)=-16
First we must interpret the information. The first part, "f''(x)<0 when x<0, f''(x)>0 when x>0," tells us that the function is concave down for x<0 and concave up for x>0. This tells us that there is a point of inflection at x=0. We will have to include this in our graph. We also note that we have two critical points. The first critical point is (-2,16) because the first derivative f'(-2) has a value of zero. Because the function is concave down for x<0, we summarize that the critical point (-2,16) is a local maximum. The second critical point is (2,-16) because the first derivative f'(2) has a value of zero. Since the function is concave up for x>0, we summarize that the critical point (2,-16) is a local minimum. Note that the problem does not tell us the value of f(0). That is, the problem tell us where the local maximum and the local minimum is located, but the problem does not tell us the co-ordinates of the point of inflection. To graph, draw a smooth curve through the local maximum and local minimum letting the point of inflection be somewhere in between at x=0. That is to say, the exact point of inflection can vary so slightly different graphs are possible. Also, make sure that the curve is concave down for all x<0 and concave up for all x>0. Below is the graph with the local minimum and local maximum.
f(x)=x⁴-2x³-12x²+3x+2
f(-1)=(-1)⁴-2(-1)³-12(-1)²+3(-1)+2
f(-1)=1+2-12-3+2
f(-1)=-10
f(x)=x⁴-2x³-12x²+3x+2
f(2)=(2)⁴-2(2)³-12(2)²+3(2)+2
f(2)=16-16-48+6+2
f(2)=-40
Therefore the function f(x)=x⁴-2x³-12x²+3x+2 has two inflection points located at (-1,10) and at (2,-40). Next, let's go through a problem where we are asked to locate local maxima and minima. When we are asked to use the second derivative test along with the critical points the problem is only concerned with the classification of the critical points. The points can be a local maximum or minimum. Note that the problem is not concerned with the intervals of concavity, as the last type of problem was.
For the following function, find the critical points. Use the second derivative test for classification.
f(x)=x³-9x²+3
The first step is to determine the critical numbers for f(x). Remember, the critical numbers are found by taking the first derivative, letting it equal zero, and solving.
f(x)=x³-9x²+3
f'(x)=3x²-18x
0=3x²-18x Let the first derivative equal zero and solve.
0=3x(x-6)
3x=0 or x-6=0
x=0 or x=6 These are our critical numbers.
Substitute our critical numbers into our original function to get our critical points. Then we can analyze using the second derivative test.
f(x)=x³-9x²+3
f(0)=(0)³-9(0)²+3
f(0)=3
f(x)=x³-9x²+3
f(6)=(6)³-9(6)²+3
f(6)=216-324+3
f(6)=-105
Now let us check these points using the second derivate test. First, we take the second derivative of f(x). Then we substitute these points into the second derivative. If the critical number yields a negative result in the second derivative test, then the curve is concave down at that point. Likewise, if the critical number yields a positive result in the second derivative test, then the curve is concave up at that point. Let us run the second derivative test on our two points.
f'(x)=3x²-18x
f''(x)=6x-18
f''(x)=6x-18
f''(0)=6(0)-18
f''(0)=-18 The curve is concave down at this point because the result is negative.
f''(x)=6x-18
f''(6)=6(6)-18
f''(6)=18 The curve is concave up at this point because the result is positive.
Note that because x=0 and x=6 are critical numbers, such that f'(0) and f'(6) are equal to zero, they constitute local maxima and minima. Since the point (0,3) lies on a curve that is concave down, it is a local maximum. Also, since the point (6,-105) lies on a curve that is concave up, it is a local minimum. Let us go through one last type of problem where we are given a set of conditions and asked to graph the function that meets all of the conditions. Note that numerous graphs are possible but you must identify the critical points and draw them on the graph to meet the conditions.
Sketch a function that satisfies all of the following conditions.
f''(x)<0 when x<0, f''(x)>0 when x>0, f'(-2)=0, f(-2)=16, f'(2)=0, f'(2)=-16
First we must interpret the information. The first part, "f''(x)<0 when x<0, f''(x)>0 when x>0," tells us that the function is concave down for x<0 and concave up for x>0. This tells us that there is a point of inflection at x=0. We will have to include this in our graph. We also note that we have two critical points. The first critical point is (-2,16) because the first derivative f'(-2) has a value of zero. Because the function is concave down for x<0, we summarize that the critical point (-2,16) is a local maximum. The second critical point is (2,-16) because the first derivative f'(2) has a value of zero. Since the function is concave up for x>0, we summarize that the critical point (2,-16) is a local minimum. Note that the problem does not tell us the value of f(0). That is, the problem tell us where the local maximum and the local minimum is located, but the problem does not tell us the co-ordinates of the point of inflection. To graph, draw a smooth curve through the local maximum and local minimum letting the point of inflection be somewhere in between at x=0. That is to say, the exact point of inflection can vary so slightly different graphs are possible. Also, make sure that the curve is concave down for all x<0 and concave up for all x>0. Below is the graph with the local minimum and local maximum.
That's all there is to know about concavity. Keep in mind that when the second derivative is negative, the original function is concave down. Likewise, if the second derivative is positive, then the original function is concave up. Also keep in mind that when the first derivative at a point is equal to zero and the second derivative is negative, there exists a local maximum. Likewise, when the first derivative at a point is equal to zero and the second derivative is positive, the exists a local minimum.
© 2020 MyMathEducator.com All Rights Reserved.