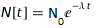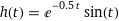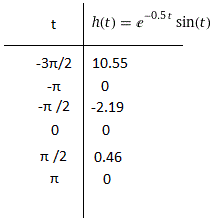Sentry Page Protection
Please Wait...
Lesson 25: Exponential Models
Exponential functions and their derivatives are important when it comes to modelling for many areas of study, including mechanical engineering, electronics, biology, environmental science, and nuclear engineering. Exponential functions can easily model the decay of radioactive materials. Radioactive materials are commonly used in energy production because when they decay, they produce a lot of energy that can be collected. Uranium-233 (U-233) for example is used in nuclear power generators for energy production. Exponential decay functions can help us understand how nuclear reactors work. The standard equation for the amount of radioactive material remaining is:
Where:
- N represents the number of radioactive nuclei at time t
- Nₒ represents the initial number of radioactive nuclei
- λ is the disintegration constant which regulates how quickly devay occurs
Note that in the equation above N and Nₒ can also represent mass and initial mass, respectively. Let us go through a sample problem where this is the case.
A 5.0 mg sample of Uranium-233 (U-233) is injected into a test tube. After 1 day in the test tube, the sample has decayed to 3.8 mg. The amount of U-233 remaining after t days is given by the function below. Determine the disintegration constant, λ, for U-233. Also determine the half-life. Then write an equation for the remaining amount in terms of its half life. Finally determine how fast the sample is decaying after 3 days.
A 5.0 mg sample of Uranium-233 (U-233) is injected into a test tube. After 1 day in the test tube, the sample has decayed to 3.8 mg. The amount of U-233 remaining after t days is given by the function below. Determine the disintegration constant, λ, for U-233. Also determine the half-life. Then write an equation for the remaining amount in terms of its half life. Finally determine how fast the sample is decaying after 3 days.
To determine the disintegration constant, substitute Nₒ=5.0, N(1)=3.8, and t=1 into the given function. (After 1 day the initial amount of 5mg has decayed to 3.8 mg). Then solve for the disintegration constant, λ.
3.8=5.0e^(-λ)(1)
3.8=5.0e^(-λ)
3.8/5.0=e^(-λ)
ln(3.8/5.0)=ln e^(-λ) Note that by taking the ln of both sides we are one step closer to the final answer because ln (e^x) = x.
-λ=ln(3.8/5.0)
λ=-ln(3.8/5.0)
λ≅0.274
Therefore the disintegration constant is about 0.27. We can now write out the equation for the amount of U-233 remaining after t days as N(t)=5e^(-0.27t). Next, let us determine the half-life. To do this we must determine how long it takes for the initial 5.0 mg sample to decay to half the amount, or 2.5 mg. That is, we must utilize the function which contains the disintegration constant and substitute N(t)=2.5mg while solving for t.
N(t)=5e^(-0.27t) Substitute N(t)=2.5 into the function and solve for t.
2.5=5e^(-0.27t)
2.5/5=e^(-0.27t)
ln (0.5)=ln e^(-0.27t) Take the natural logarithm of both sides. Note that ln e^(-0.27t) = -0.27t.
-0.27t=ln (0.5)
t=[ln (0.5)]/-0.27
t≅2.57
Therefore the half-life of U-233 is approximately 2.6 days. Next we are asked to write an equation for the remaining amount in terms of the half-life. This can be easily done if we use the factor 1/2 raised to t/2.6 because t must be expressed in terms of the number of half-lifes. The equation that expresses the remaining amount of U-233 in terms of half lifes, where N(t) represents the remaining amount and t is the elapsed number of days is:
N(t)=5[(1/2)^(t/2.6)]
The fact that we could model the decay of U-233 in another way reveals that exponential models can be presented in different ways. The choice of model depends on the problem being solved. Finally we are asked how fast the sample is decaying after 3 days. To determine this, we must take the derivative of the original function and solve for t=3:
N(t)=5e^-0.27t
N'(t)=(-0.27)5e^-0.27t
N'(3)=(-0.27)5e^-0.27(3)
N'(3)≅-0.60
After 3 days the sample of U-233 is decaying at a rate of about 0.60 mg per day. Composite functions involving exponentials occur in engineering and other areas in science. Let us look at a problem from mechanical engineering:
The motion of a harmonic oscillator repeats over regular intervals of time. When the amplitude of the motion decreases over time because of friction, the motion is damped harmonic motion. The vertical displacement of a car as it passes over a speed bump is modelled by the function given below, where h is vertical displacement in meters, after t seconds. Graph the function, describing its shape. Determine when the maximum vertical displacement of the car occurs. Then determine the maximum displacement at that time.
3.8=5.0e^(-λ)(1)
3.8=5.0e^(-λ)
3.8/5.0=e^(-λ)
ln(3.8/5.0)=ln e^(-λ) Note that by taking the ln of both sides we are one step closer to the final answer because ln (e^x) = x.
-λ=ln(3.8/5.0)
λ=-ln(3.8/5.0)
λ≅0.274
Therefore the disintegration constant is about 0.27. We can now write out the equation for the amount of U-233 remaining after t days as N(t)=5e^(-0.27t). Next, let us determine the half-life. To do this we must determine how long it takes for the initial 5.0 mg sample to decay to half the amount, or 2.5 mg. That is, we must utilize the function which contains the disintegration constant and substitute N(t)=2.5mg while solving for t.
N(t)=5e^(-0.27t) Substitute N(t)=2.5 into the function and solve for t.
2.5=5e^(-0.27t)
2.5/5=e^(-0.27t)
ln (0.5)=ln e^(-0.27t) Take the natural logarithm of both sides. Note that ln e^(-0.27t) = -0.27t.
-0.27t=ln (0.5)
t=[ln (0.5)]/-0.27
t≅2.57
Therefore the half-life of U-233 is approximately 2.6 days. Next we are asked to write an equation for the remaining amount in terms of the half-life. This can be easily done if we use the factor 1/2 raised to t/2.6 because t must be expressed in terms of the number of half-lifes. The equation that expresses the remaining amount of U-233 in terms of half lifes, where N(t) represents the remaining amount and t is the elapsed number of days is:
N(t)=5[(1/2)^(t/2.6)]
The fact that we could model the decay of U-233 in another way reveals that exponential models can be presented in different ways. The choice of model depends on the problem being solved. Finally we are asked how fast the sample is decaying after 3 days. To determine this, we must take the derivative of the original function and solve for t=3:
N(t)=5e^-0.27t
N'(t)=(-0.27)5e^-0.27t
N'(3)=(-0.27)5e^-0.27(3)
N'(3)≅-0.60
After 3 days the sample of U-233 is decaying at a rate of about 0.60 mg per day. Composite functions involving exponentials occur in engineering and other areas in science. Let us look at a problem from mechanical engineering:
The motion of a harmonic oscillator repeats over regular intervals of time. When the amplitude of the motion decreases over time because of friction, the motion is damped harmonic motion. The vertical displacement of a car as it passes over a speed bump is modelled by the function given below, where h is vertical displacement in meters, after t seconds. Graph the function, describing its shape. Determine when the maximum vertical displacement of the car occurs. Then determine the maximum displacement at that time.
To graph the function, calculate a set of ordered pairs:
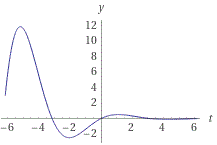
Now simply draw a smooth curve through all of the points:
We must determine when the maximum vertical displacement of the car occurs. This will be a local maximum or minimum so we need to take the first derivative and solve:
h(t)=e^(-0.5t)[sin t]
h'(t)=d/dt[e^(-0.5t)][sin t]+[e^(-0.5t)]d/dt[sin t]
h'(t)=(-0.5)[e^(-0.5t)][sin t]+[e^(-0.5t)][cos t]
h'(t)=[e^(-0.5t)][-0.5 sin t + cos t]
h'(t)=[e^(-0.5t)][cos t - 0.5 sin t]
Set h'(t) equal to zero and solve for t:
0=[e^(-0.5t)][cos t - 0.5 sin t]
Case 1:
e^(-0.5t)=0
This has no solution because e raised to any number will always be a positive number. It will never be equal to zero.
Case 2:
cos t - 0.5 sin t=0
cos t=0.5 sin t Divide both sides by cos t. Since sin t/cos t= tan t, we now have only one t to isolate.
1=0.5 tan t
2= tan t
t≅1.11 Use your scientific calculator to isolate t by taking the inverse. Make sure the setting is on Radian mode.
Therefore the maximum vertical displacement occurs approximately 1.11 seconds after going over the speed bump. Note that this result makes sense because there is a local maximum on the graph between 1 and 2. Note also that this is clearly the maximum vertical displacement for all values of t greater than zero.
h(t)=e^(-0.5t)[sin t]
h'(t)=d/dt[e^(-0.5t)][sin t]+[e^(-0.5t)]d/dt[sin t]
h'(t)=(-0.5)[e^(-0.5t)][sin t]+[e^(-0.5t)][cos t]
h'(t)=[e^(-0.5t)][-0.5 sin t + cos t]
h'(t)=[e^(-0.5t)][cos t - 0.5 sin t]
Set h'(t) equal to zero and solve for t:
0=[e^(-0.5t)][cos t - 0.5 sin t]
Case 1:
e^(-0.5t)=0
This has no solution because e raised to any number will always be a positive number. It will never be equal to zero.
Case 2:
cos t - 0.5 sin t=0
cos t=0.5 sin t Divide both sides by cos t. Since sin t/cos t= tan t, we now have only one t to isolate.
1=0.5 tan t
2= tan t
t≅1.11 Use your scientific calculator to isolate t by taking the inverse. Make sure the setting is on Radian mode.
Therefore the maximum vertical displacement occurs approximately 1.11 seconds after going over the speed bump. Note that this result makes sense because there is a local maximum on the graph between 1 and 2. Note also that this is clearly the maximum vertical displacement for all values of t greater than zero.
Next we are asked what the maximum displacement is. We already know that the maximum displacement occurs at t=1.11. To determine the maximum displacement, simply substitute t=1.11 into the original equation for displacement:
h(t)=e^(-0.5t)[sin t]
h(1.11)=e^(-0.5(1.11))[sin (1.11)]
h(1.11)=(0.574072261)(0.895698685)
h(1.11)≅0.5142
Therefore the maximum vertical displacement of the car is 0.51 m. That's all for this lesson and for this portion of the course. Take your time and review any problems you did not understand and be sure to get plenty of practice. Practice makes perfect!
h(t)=e^(-0.5t)[sin t]
h(1.11)=e^(-0.5(1.11))[sin (1.11)]
h(1.11)=(0.574072261)(0.895698685)
h(1.11)≅0.5142
Therefore the maximum vertical displacement of the car is 0.51 m. That's all for this lesson and for this portion of the course. Take your time and review any problems you did not understand and be sure to get plenty of practice. Practice makes perfect!
© 2020 MyMathEducator.com All Rights Reserved