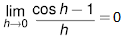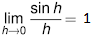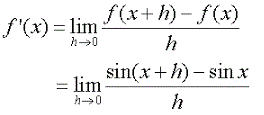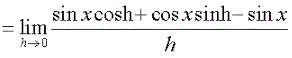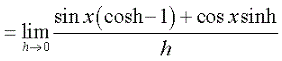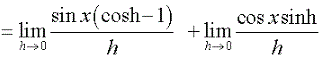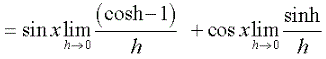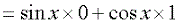Sentry Page Protection
Please Wait...
Lesson 18: Derivatives of the Sine and Cosine Functions
Sinusoidal functions are functions that have graphs with the shape of a sine wave. There are many applications of such functions in everyday life. X-rays, infrared, radio, cell phone, and television electromagnetic waves can all be modelled by sinusoidal functions. The rate of change of a sinusoidal function is periodic. This means that it repeats itself as it goes through a cycle. Note also that the derivative of a sinusoidal function is also a sinusoidal function. We will quickly go over the full proof of the sine derivative but before we do that it is important that you know the following two limits as they will be utilized in the proof. (They are more advanced limits, so you do not need to know how to prove them),
To begin our proof, we use the first principles definition to take the derivative of f(x)=sin x. Remember, the formula for the first principle definition allows us to take the derivative of any function f(x). If f(x)= sin x, then f(x+h)= sin (x+h). Substitute into the formula:
Next, we use the identity sin(a+b)= sin a cos b + cos a sin b on sin(x+h):
Next we re-arrange the terms so that the numerator reads sin x cos h - sin x + cos x sin h. This will allow for the factoring of sin x from the first two terms:
The next steps consist of breaking up f'(x) as a sum of limits. We remember that the limit of a sum is the sum of the limits. As a result, we can break up our problem into a sum and apply the limit to each part of the sum.
Because sin x and cos x are fixed and do not depend on h, they can be placed as factors to the left of the limits.
Substitute the values for the limits shown above. Then simplify to get the derivative of sin x.
=cos x
Therefore, the derivative of y=sin x is dy/dx=cos x. To determine the derivative of y= cos x we can use the above calculation and the difference identity:
y= cos x
= sin (π/2-x) Per the difference identity, cos x = sin (π/2-x).
Therefore, the derivative of y=sin x is dy/dx=cos x. To determine the derivative of y= cos x we can use the above calculation and the difference identity:
y= cos x
= sin (π/2-x) Per the difference identity, cos x = sin (π/2-x).
To differentiate, we will use what we just learned. That is, we know that the derivative of sin x is cos x. We will therefore apply this, but we will not forget the chain rule since sin (π/2-x) is a function acting on a function. If we take the derivative of the internal part (π/2-x), we get -1.
dy/dx = cos (π/2-x) d/dx(π/2-x) Note that we applied the rule we just learned in taking the derivative of the sine function to get a cosine function.
dy/dx = sin x (-1) Note that cos (π/2-x)= sin x. We also remembered to use the chain rule. The derivative of π/2-x is -1.
dy/dx = - sin x
Therefore, the derivative of y=cos x is dy/dx= -sin x. Note that all of the rules of differentiation can be applied to sinusoidal functions. This includes the constant multiple rule. Let's run though some problems where we use derivatives on sinusoidal functions.
Find the derivative of f(x)=-5cos x.
Note that we already know that the derivative of cos x is sin x, but we have a coefficient of -5, so we have to apply the constant multiple rule.
f(x)=-5cos x
f(x)=-5(-sin x) The derivative of cos x is -sin x. Apply the constant multiple rule.
f(x)= 5sin x
Let's run through another problem.
Find the derivative of f(x)=3sin x - 5cos x.
f(x)=3sin x - 5cos x
f'(x)=3(cos x) - 5(-sin x) Apply the difference and the constant multiple rule.
f(x)=3cos x + 5sin x
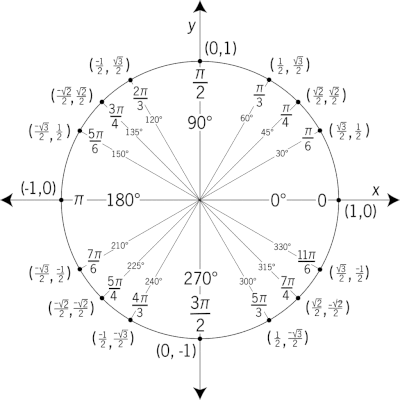
Next we will run through a problem that requires us to know the values of sine and cosine for some basic angles on the unit circle. It is a good idea to memorize the unit circle so that you are not constantly referencing it.
dy/dx = cos (π/2-x) d/dx(π/2-x) Note that we applied the rule we just learned in taking the derivative of the sine function to get a cosine function.
dy/dx = sin x (-1) Note that cos (π/2-x)= sin x. We also remembered to use the chain rule. The derivative of π/2-x is -1.
dy/dx = - sin x
Therefore, the derivative of y=cos x is dy/dx= -sin x. Note that all of the rules of differentiation can be applied to sinusoidal functions. This includes the constant multiple rule. Let's run though some problems where we use derivatives on sinusoidal functions.
Find the derivative of f(x)=-5cos x.
Note that we already know that the derivative of cos x is sin x, but we have a coefficient of -5, so we have to apply the constant multiple rule.
f(x)=-5cos x
f(x)=-5(-sin x) The derivative of cos x is -sin x. Apply the constant multiple rule.
f(x)= 5sin x
Let's run through another problem.
Find the derivative of f(x)=3sin x - 5cos x.
f(x)=3sin x - 5cos x
f'(x)=3(cos x) - 5(-sin x) Apply the difference and the constant multiple rule.
f(x)=3cos x + 5sin x
Next we will run through a problem that requires us to know the values of sine and cosine for some basic angles on the unit circle. It is a good idea to memorize the unit circle so that you are not constantly referencing it.
Remember, the first value in each parenthesis is the cosine value for the respective angle and the second value is the sine value. With this in mind, let us proceed.
Find the slope of the line tangent to the graph at f(x)= 4cos x at the point where x=π/6.
Find the slope of the line tangent to the graph at f(x)= 4cos x at the point where x=π/6.
To find the slope of a line tangent to any graph at a particular value, we simply take the derivative and solve for the respective value.
f(x)= 4cos x
f'(x)= 4(-sin x)
f'(x)= -4 sin x
Now solve for x=π/6:
f'(π/6)= -4 sin π/6
f'(π/6)= -4 (1/2)
f'(π/6)= -2
Therefore the slope of the tangent line to the graph at x=π/6 is -2. Let's run through another similar problem.
Find the equation of the line tangent to f(x)=-3cos x at x=π/3.
To solve this type of problem we again find the slope of the tangent at the specific point by substituting the point into the derivative. This gives us the slope, but in this type of problem we want the entire equation. As a result, we also have to solve for the co-ordinates at the point in question. Once this is done we can substitute the slope and the point into the point-slope formula of a line.
We begin by solving for the value of the derivative at x=π/3.
f(x)=-3cos x
f'(x)=-3(-sin x)
f'(x)=3sin x
f'(π/3)=3sin (π/3)
f'(π/3)=3(√3/2)
f'(π/3)=(3√3)/2
Next, let us solve for the point of tangency by substituting x=π/3 into the function f(x)=-3cos x.
f(x)=-3cos x
f(π/3)=-3cos (π/3)
f(π/3)=-3 (1/2)
f(π/3)=-3/2
Therefore the point of tangency is (π/3,-3/2). Next, we substitute this point and the slope we just computed into the point-slope formula:
y-y₁=m(x-x₁)
y-(-3/2)=(3√3)/2(x-π/3) x₁=π/3, y₁=-3/2, and m=(3√3)/2
y+3/2=(3√3)/2(x-π/3)
y=(3√3x)/2-(3√3π)/3-3/2
y=(3√3x)/2-√3π-3/2
Therefore the equation of the tangent line at x=π/3 is y=(3√3x)/2-√3π-3/2. Note that we cannot simplify the answer any more, so we just leave it as it is. Also, note that you will be using the values from the unit circle quite often, so it helps to memorize them. That's all there is to know for this lesson.
f(x)= 4cos x
f'(x)= 4(-sin x)
f'(x)= -4 sin x
Now solve for x=π/6:
f'(π/6)= -4 sin π/6
f'(π/6)= -4 (1/2)
f'(π/6)= -2
Therefore the slope of the tangent line to the graph at x=π/6 is -2. Let's run through another similar problem.
Find the equation of the line tangent to f(x)=-3cos x at x=π/3.
To solve this type of problem we again find the slope of the tangent at the specific point by substituting the point into the derivative. This gives us the slope, but in this type of problem we want the entire equation. As a result, we also have to solve for the co-ordinates at the point in question. Once this is done we can substitute the slope and the point into the point-slope formula of a line.
We begin by solving for the value of the derivative at x=π/3.
f(x)=-3cos x
f'(x)=-3(-sin x)
f'(x)=3sin x
f'(π/3)=3sin (π/3)
f'(π/3)=3(√3/2)
f'(π/3)=(3√3)/2
Next, let us solve for the point of tangency by substituting x=π/3 into the function f(x)=-3cos x.
f(x)=-3cos x
f(π/3)=-3cos (π/3)
f(π/3)=-3 (1/2)
f(π/3)=-3/2
Therefore the point of tangency is (π/3,-3/2). Next, we substitute this point and the slope we just computed into the point-slope formula:
y-y₁=m(x-x₁)
y-(-3/2)=(3√3)/2(x-π/3) x₁=π/3, y₁=-3/2, and m=(3√3)/2
y+3/2=(3√3)/2(x-π/3)
y=(3√3x)/2-(3√3π)/3-3/2
y=(3√3x)/2-√3π-3/2
Therefore the equation of the tangent line at x=π/3 is y=(3√3x)/2-√3π-3/2. Note that we cannot simplify the answer any more, so we just leave it as it is. Also, note that you will be using the values from the unit circle quite often, so it helps to memorize them. That's all there is to know for this lesson.
© 2020 MyMathEducator.com All Rights Reserved.