Lesson 5: Solving Quadratic Equations
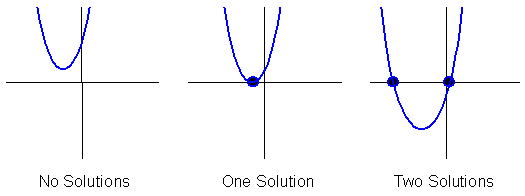
Solving a quadratic equation is an important skill in mathematics and in this course. A quadratic equation is simply any equation of the form ax²+bx+c=0, where a, b, and c are all real numbers and a≠ 0. As a result the equation has a degree of 2. All solving quadratic equations means finding the zeroes, or the x-intercepts. There may be two solutions to a quadratic equation, one solution, or no solutions. To solve a quadratic equation you can use one of three formulas: you can complete the square, factor, or use the quadratic formula. When completing the square make y=0, so that you can find the x=intercepts. Let's look at an example:
y= 2x²+12x+7
0= 2x²+12x+7
0= 2(x²+6x)+7
0= 2(x²+6x+9-9)+7
0= 2(x²+6x+9)-18+7
0= 2(x+3)² -11
Now all that must be done is to isolate the x-term. This will give you the x-intercepts of the quadratic equation.
0= 2(x+3)² -11 Add eleven to both sides.
11=2(x+3)² Divide both sides by 2.
11/2=(x+3)² Find the square root of both sides. Remember there will be two roots, a positive and a negative one.
+/-√11/2=x+3 Subtract three from both sides.
+/-√11/2-3=x
Therefore the two solutions are √11/2-3 and -√11/2-3. Notice that we use rational numbers and radicals; we want our answers to be exact.
If it is possible, you may be able to simply factor the equation. Then use the AB rule, which states that if two numbers are multiplied to give zero, at least one is zero. Lets look at an example.
y=x²+2x+1 Let y=0
0=x²+2x+1 Factor the equation. it is a perfect square trinomial.
0=(x+1)(x+1) Isolate x in each factor on the left side.
x=-1
Therefore, the solution is -1.
Lastly you could use the quadratic formula. The quadratic equation is handy because it gives exact answers and because you simply need to plug the values of a. b, and c into the quadratic formula.
x=(-b+/-√[b²-4ac]/2a)
Let's find the value of a, b, and c in the above equation.
y=x²+2x+1
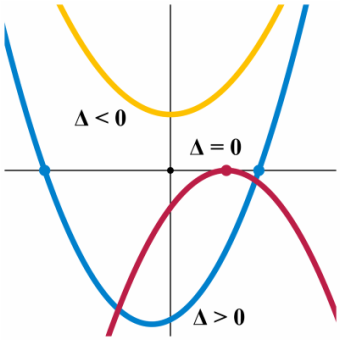
a=1, b=2, and c=1. If you wish to find out how many solutions there are to a particular equation, there is a simple formula to find the number of solutions, also known as the discriminant. The discriminant is :
b²-4ac. If b²-4ac>0, there are two solutions, if b²-4ac=0, there is only one solution, and if b²-4ac<0, there are no solutions.
Let's use the above equation and check how many solutions there are:
y=x²+2x+1
a=1, b=2, c=1
b²-4ac
=(2)²-4(1)(1)
=4-4
=0
Since the discriminant is 0, the quadratic equation has only one solution.
y= 2x²+12x+7
0= 2x²+12x+7
0= 2(x²+6x)+7
0= 2(x²+6x+9-9)+7
0= 2(x²+6x+9)-18+7
0= 2(x+3)² -11
Now all that must be done is to isolate the x-term. This will give you the x-intercepts of the quadratic equation.
0= 2(x+3)² -11 Add eleven to both sides.
11=2(x+3)² Divide both sides by 2.
11/2=(x+3)² Find the square root of both sides. Remember there will be two roots, a positive and a negative one.
+/-√11/2=x+3 Subtract three from both sides.
+/-√11/2-3=x
Therefore the two solutions are √11/2-3 and -√11/2-3. Notice that we use rational numbers and radicals; we want our answers to be exact.
If it is possible, you may be able to simply factor the equation. Then use the AB rule, which states that if two numbers are multiplied to give zero, at least one is zero. Lets look at an example.
y=x²+2x+1 Let y=0
0=x²+2x+1 Factor the equation. it is a perfect square trinomial.
0=(x+1)(x+1) Isolate x in each factor on the left side.
x=-1
Therefore, the solution is -1.
Lastly you could use the quadratic formula. The quadratic equation is handy because it gives exact answers and because you simply need to plug the values of a. b, and c into the quadratic formula.
x=(-b+/-√[b²-4ac]/2a)
Let's find the value of a, b, and c in the above equation.
y=x²+2x+1
a=1, b=2, and c=1. If you wish to find out how many solutions there are to a particular equation, there is a simple formula to find the number of solutions, also known as the discriminant. The discriminant is :
b²-4ac. If b²-4ac>0, there are two solutions, if b²-4ac=0, there is only one solution, and if b²-4ac<0, there are no solutions.
Let's use the above equation and check how many solutions there are:
y=x²+2x+1
a=1, b=2, c=1
b²-4ac
=(2)²-4(1)(1)
=4-4
=0
Since the discriminant is 0, the quadratic equation has only one solution.
© 2020 MyMathEducator.com All Rights Reserved.