Lesson 3: Maximum or Minimum of a Quadratic Function
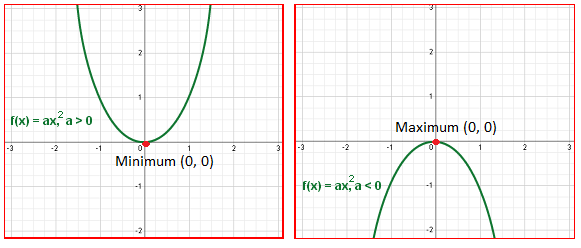
A quadratic function can be expressed in standard form, in factored form, or in vertex form. In standard form, f(x)=ax²+bx+c, c is the y-intercept. You can verify this by substituting x=0 into the function. In factored form, f(x)=a(x-r)(x-s), the x-intercepts are r and s. In vertex form, f(x)= a(x-h)²+k, the vertex is (h,k). The sign of the coefficient a in these functions dictates the direction of opening of the parabola. if a>0, the parabola opens upwards and the vertex is a minimum. If a<0, the parabola opens downward and the vertex is a maximum.
In order to determine the vertex of a quadratic function, it must be expressed in vertex form. If you are given a quadratic equation in factored form, convert it to standard form by simplifying. Once in standard form, you must convert the function to vertex form through a process known as "completing the square". Let's go through an example:
f(x)= 2x²+12x+7
First, insure that the x² term has no co-efficient. If it does, factor it from the first two terms.
f(x)= 2x²+12x+7
f(x)= 2(x²+6x)+7
Then divide the coefficient of the x term by two, square it, and add it to the x term to make a perfect square trinomial. Then subtract the same term so that the value of the function remains the same; adding and subtracting a number does not change the value of an equation.
f(x)= 2x²+12x+7
f(x)= 2(x²+6x)+7
f(x)= 2(x²+6x+9-9)+7
Now you must remove the constant that you subtracted, so that you are left with a perfect square trinomial in the bracket. To do this multiply the negative constant with the value in front of the brackets, two in this case. Then add this to the constant term after the bracket.
f(x)= 2x²+12x+7
f(x)= 2(x²+6x)+7
f(x)= 2(x²+6x+9-9)+7
f(x)= 2(x²+6x+9)-18+7
f(x)= 2(x²+6x+9)-11
Finally, factor the perfect square trinomial:
f(x)= 2(x+3)² -11
Therefore, the vertex is (-3,-11). Another way of finding the vertex of a quadratic formula is to use partial factoring to find the x-intercepts. The vertex can then be found; the vertex is on the line of symmetry of a quadratic function, or halfway between the x-intercepts. Since the third term only affects the vertical position of a parabola, we only need to factor the first two terms. Let's look at an example. Suppose we wanted to find the vertex of the following quadratic equation:
y=6x²-12x+5
In order to find the x-intercepts, we must factor the first two terms:
y=6x²-12x+5
y=6x²-12x
y=6x(x-2)
When y=0: (To find x-intercepts)
0=6x(x-2)
6x=0 or x-2=0
x=0 or x=2
Next, find the average of the two x-intercepts to give you the x-coordinate of the vertex for y=6x²-12x+5. (The x-coordinate of the vertex of the two equations will be the same.)
0+2/2=2/2=1
The x-coordinate of the vertex is 1. To find the y-coordinate of the vertex of the quadratic function y=6x²-12x+5 simply substitute x=1 into the equation.
y=6x²-12x+5
y=6(1)²-12(1)+5
y=6(1)-12+5
y=6-12+5
y=-1
The vertex of the function y=6x² -12x+5 is located at (1, -1)
Using one of the methods listed above, solving a word problem involving a minimum or maximum is fairly simple. First, identify what the problem is asking. Write a quadratic function, if necessary, and find it's vertex. Remember to conclude with an answer statement. Lets look at a word problem:
Raheem and Sanjit create jewellery each summer for a local fair. Last summer they sold 100 pieces of jewellery at $15 each. They know that for each one dollar increase in price, they will sell 5 fewer pieces of jewellery. What price will maximize revenue?
First write a let statement and create a quadratic equation to represent the situation.
Let x represent the number of $1 changes and let y represent the revenue, in dollars.
Revenue= price per jewellery*number sold
y=(15+x)(100-5x)
y=-5x²+25x+1500
Complete the square:
y=-5x²+25x+1500
y=-5(x²-5x)+1500
y=-5(x²-5x+(5/2)²-(5/2)²)+1500
y=-5(x²-5x+25/4-25/4)+1500
y=-5(x²-5x+25/4)+125/4+1500
y=-5(x-5/2)²+6125/4
y=-5(x-5/2)²+1531.25
The vertex is a maximum at (5/2, 1531.25)
As a result, 5/2 increases of $1 will maximize revenue.
5/2*1=2.5
An increase of $2.50 to $17.50 will maximize revenue. (Note that the x-value represents the number of $1 increases needed to maximize revenue)
f(x)= 2x²+12x+7
First, insure that the x² term has no co-efficient. If it does, factor it from the first two terms.
f(x)= 2x²+12x+7
f(x)= 2(x²+6x)+7
Then divide the coefficient of the x term by two, square it, and add it to the x term to make a perfect square trinomial. Then subtract the same term so that the value of the function remains the same; adding and subtracting a number does not change the value of an equation.
f(x)= 2x²+12x+7
f(x)= 2(x²+6x)+7
f(x)= 2(x²+6x+9-9)+7
Now you must remove the constant that you subtracted, so that you are left with a perfect square trinomial in the bracket. To do this multiply the negative constant with the value in front of the brackets, two in this case. Then add this to the constant term after the bracket.
f(x)= 2x²+12x+7
f(x)= 2(x²+6x)+7
f(x)= 2(x²+6x+9-9)+7
f(x)= 2(x²+6x+9)-18+7
f(x)= 2(x²+6x+9)-11
Finally, factor the perfect square trinomial:
f(x)= 2(x+3)² -11
Therefore, the vertex is (-3,-11). Another way of finding the vertex of a quadratic formula is to use partial factoring to find the x-intercepts. The vertex can then be found; the vertex is on the line of symmetry of a quadratic function, or halfway between the x-intercepts. Since the third term only affects the vertical position of a parabola, we only need to factor the first two terms. Let's look at an example. Suppose we wanted to find the vertex of the following quadratic equation:
y=6x²-12x+5
In order to find the x-intercepts, we must factor the first two terms:
y=6x²-12x+5
y=6x²-12x
y=6x(x-2)
When y=0: (To find x-intercepts)
0=6x(x-2)
6x=0 or x-2=0
x=0 or x=2
Next, find the average of the two x-intercepts to give you the x-coordinate of the vertex for y=6x²-12x+5. (The x-coordinate of the vertex of the two equations will be the same.)
0+2/2=2/2=1
The x-coordinate of the vertex is 1. To find the y-coordinate of the vertex of the quadratic function y=6x²-12x+5 simply substitute x=1 into the equation.
y=6x²-12x+5
y=6(1)²-12(1)+5
y=6(1)-12+5
y=6-12+5
y=-1
The vertex of the function y=6x² -12x+5 is located at (1, -1)
Using one of the methods listed above, solving a word problem involving a minimum or maximum is fairly simple. First, identify what the problem is asking. Write a quadratic function, if necessary, and find it's vertex. Remember to conclude with an answer statement. Lets look at a word problem:
Raheem and Sanjit create jewellery each summer for a local fair. Last summer they sold 100 pieces of jewellery at $15 each. They know that for each one dollar increase in price, they will sell 5 fewer pieces of jewellery. What price will maximize revenue?
First write a let statement and create a quadratic equation to represent the situation.
Let x represent the number of $1 changes and let y represent the revenue, in dollars.
Revenue= price per jewellery*number sold
y=(15+x)(100-5x)
y=-5x²+25x+1500
Complete the square:
y=-5x²+25x+1500
y=-5(x²-5x)+1500
y=-5(x²-5x+(5/2)²-(5/2)²)+1500
y=-5(x²-5x+25/4-25/4)+1500
y=-5(x²-5x+25/4)+125/4+1500
y=-5(x-5/2)²+6125/4
y=-5(x-5/2)²+1531.25
The vertex is a maximum at (5/2, 1531.25)
As a result, 5/2 increases of $1 will maximize revenue.
5/2*1=2.5
An increase of $2.50 to $17.50 will maximize revenue. (Note that the x-value represents the number of $1 increases needed to maximize revenue)
© 2020 MyMathEducator.com All Rights Reserved.