Lesson 1: Functions, Domain, and Range
Key Terms
Relation- an identified pattern between two variables that may be represented as ordered pairs, a table of values, a graph, or an equation.
Function- a relation in which each value of the independent variable matches with exactly one value of the dependent variable.
What is a function? A function is any relation in which each independent variable matches with exactly one dependent variable. As you know, a relation is any pattern or relationship between two values. It can be represented through ordered pairs, a table of values, a graph or an equation. As a result all functions are relations (all functions relate two variables), but not all relations are functions. If a relation has two dependent variables for any independent variable, it is not a function. If all the independent variables correspond with exactly one dependent variable, then the relation is a function.
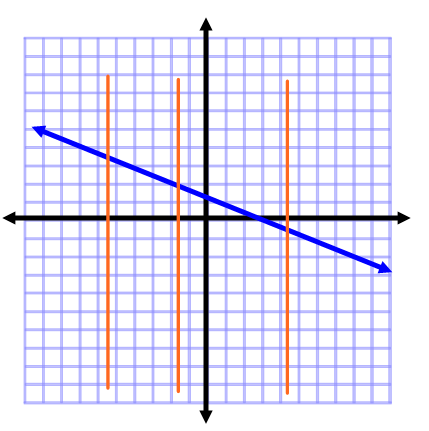
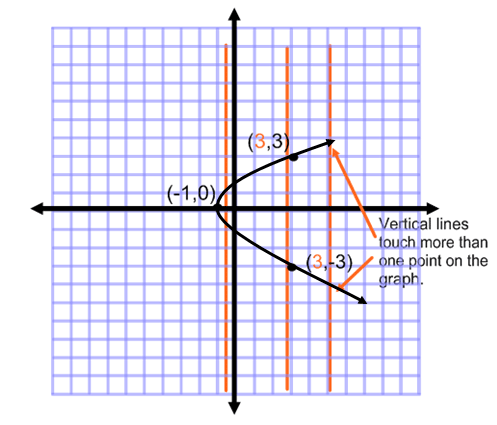
So how can you tell if a relation is a function? there are numerous ways of telling if a relation is a function, depending on the way the relation is displayed (table of values, ordered pairs, graph etc.). If the relation is displayed through a graph, you can use the vertical line test to verify if it is a function. If every vertical line drawn through a function intersects the relation at exactly one point, then the relation is a function. If a vertical line intersects the relation at two or more points, then the relation is not a function.
Relation- an identified pattern between two variables that may be represented as ordered pairs, a table of values, a graph, or an equation.
Function- a relation in which each value of the independent variable matches with exactly one value of the dependent variable.
What is a function? A function is any relation in which each independent variable matches with exactly one dependent variable. As you know, a relation is any pattern or relationship between two values. It can be represented through ordered pairs, a table of values, a graph or an equation. As a result all functions are relations (all functions relate two variables), but not all relations are functions. If a relation has two dependent variables for any independent variable, it is not a function. If all the independent variables correspond with exactly one dependent variable, then the relation is a function.
So how can you tell if a relation is a function? there are numerous ways of telling if a relation is a function, depending on the way the relation is displayed (table of values, ordered pairs, graph etc.). If the relation is displayed through a graph, you can use the vertical line test to verify if it is a function. If every vertical line drawn through a function intersects the relation at exactly one point, then the relation is a function. If a vertical line intersects the relation at two or more points, then the relation is not a function.
The above relation is a function because every vertical line drawn through it intersects it at exactly one point. No vertical line can be drawn through more than one point on the relation. The graph below is not a relation because a vertical line drawn through it intersects it at more than one point. Therefore, at least one independent variable corresponds with more than one dependent variable. As a result, it is not a function.
Domain and Range
For any relation, the set of values of the independent variable (often x-values) is called the domain of the relation. The set of corresponding dependent variables (often y-axis) are called the range of a relation. In a function, each value in the domain corresponds with exactly one value in the range. If a value in the domain has more than one corresponding value in the range, then the relation is not a function. With this knowledge you can determine is the relation displayed through a set of data is a function or not.
For example, if you are given the set of ordered pairs,
{(-3, 4), (5, -6), (-2, 7), (5, 3), (6, -8)},
you can determine if any value in the domain corresponds with more than one value in the range. First, find the domain and the range for the entire set. The domain is the set of independent variables, or the x-co-ordinates in this case. The range is the set of dependent variables, or the y-co-ordinates in this case.
Use curly brackets ({ }) to enclose numbers in a set. Therefore, the domain and range would be:
domain {-3, -2, 5, 6}, range {-8, -6, 3, 4, 7}.
Note how the numbers are placed in increasing order. Now compare thee numbers of terms in the range with the number of terms in the domain. If there are more terms in the range than in the domain, then you know that at least one term in the domain corresponds with more than one term in the range. Consequently, the relation is not a function. Let us look at our relation:
domain {-3, -2, 5, 6}, range {-8, -6, 3, 4, 7}.
Since there are five terms in the range and only four terms in the domain, the relation is not a function. If their domain has more than, or an equal number of terms as the range, then the relation is a function.
The domain and range of equations can also be expressed through set notation. The domain and range of an equation can be found by seeing what values cannot exist for the particular equation. These restrictions are then stated in the domain and the range of the equation. Restrictions on the domain include dividing by zero and when an expression under a radical sign is negative; these cases cannot exist.
The range of the function can be determined by the shape of the graph of the function.
For example, if you are given the set of ordered pairs,
{(-3, 4), (5, -6), (-2, 7), (5, 3), (6, -8)},
you can determine if any value in the domain corresponds with more than one value in the range. First, find the domain and the range for the entire set. The domain is the set of independent variables, or the x-co-ordinates in this case. The range is the set of dependent variables, or the y-co-ordinates in this case.
Use curly brackets ({ }) to enclose numbers in a set. Therefore, the domain and range would be:
domain {-3, -2, 5, 6}, range {-8, -6, 3, 4, 7}.
Note how the numbers are placed in increasing order. Now compare thee numbers of terms in the range with the number of terms in the domain. If there are more terms in the range than in the domain, then you know that at least one term in the domain corresponds with more than one term in the range. Consequently, the relation is not a function. Let us look at our relation:
domain {-3, -2, 5, 6}, range {-8, -6, 3, 4, 7}.
Since there are five terms in the range and only four terms in the domain, the relation is not a function. If their domain has more than, or an equal number of terms as the range, then the relation is a function.
The domain and range of equations can also be expressed through set notation. The domain and range of an equation can be found by seeing what values cannot exist for the particular equation. These restrictions are then stated in the domain and the range of the equation. Restrictions on the domain include dividing by zero and when an expression under a radical sign is negative; these cases cannot exist.
The range of the function can be determined by the shape of the graph of the function.
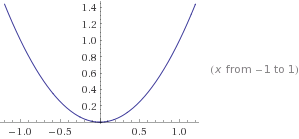
For the graph above, y=x^2, there are no restrictions on the possible values of x. In effect, x-can be any real number (any rational/irrational number). Therefore the domain is written as:
domain {xεR} (this reads as: the domain belongs to all real numbers).
Since the graph of the parabola has y-values greater than or equal to zero the range is as follows:
range {yεR, y≥0}
Note the restriction on the range which states that the y-values must be greater than or equal to zero. In some cases a function has only one value in which the domain or the range is restricted. This is known as an asymptote. An asymptote is a line which a curve comes closer and closer to , but never touches it. Let's look at one example:
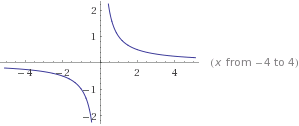
y=1/x
domain {xεR} (this reads as: the domain belongs to all real numbers).
Since the graph of the parabola has y-values greater than or equal to zero the range is as follows:
range {yεR, y≥0}
Note the restriction on the range which states that the y-values must be greater than or equal to zero. In some cases a function has only one value in which the domain or the range is restricted. This is known as an asymptote. An asymptote is a line which a curve comes closer and closer to , but never touches it. Let's look at one example:
y=1/x
In the graph above the domain is restricted by the fact that x cannot be zero; division by zero is impossible. Since, 1 cannot be divided by zero, there also will be a restriction for zero in the range. The graph above clearly shows this because it gets closer and closer to the lines x=0 and y=0, but it never actually touches them.
domain {xεR, x≠0} range {yεR, y≠0}. The asymptotes for this graph are x=0 and y=0.
domain {xεR, x≠0} range {yεR, y≠0}. The asymptotes for this graph are x=0 and y=0.
© 2020 MyMathEducator.com All Rights Reserved.